
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
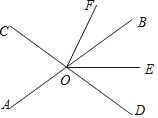
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)若|∠AOC﹣∠BOF|=α°,请直接写出∠AOC和∠BOF的度数.(用含的代数式表示)
【答案】(1)∠BOF=33°;(2)∠AOC=72°;(3) ∠AOC=2x=(![]() )°﹣
)°﹣![]() α°,∠BOF=(
α°,∠BOF=(![]() )°+
)°+![]() α°.
α°.
【解析】试题分析:
(1)由∠AOC=76°易得∠BOD=76°,结合OE平分∠BOD可得∠DOE=∠BOE=38°,由此可得∠COE=180°-38°=142°,结合OF平分∠COE可得∠EOF=71°,最后由∠BOF=∠EOF-∠BOE即可求得∠BOF的度数;
(2)设∠BOE=x,由OE平分∠BOD,∠AOC=∠BOD可得∠DOE=∠BOE=x,∠AOC=2x,结合∠BOF=36°,OF平均∠EOF可得∠COF=∠EOF=x+36°,最后由∠AOC+∠COF+∠BOF=180°即可列出关于x的方程,解方程求得x的值即可求得∠AOC的度数;
(3)设∠BOE=x,则由已知条件易得∠AOC=2x,∠BOF=90°-![]() x,这样结合|∠AOC﹣∠BOF|=α°即可列出关于x的方程,解方程求得x的值即可求得∠AOC和∠BOF的值.
x,这样结合|∠AOC﹣∠BOF|=α°即可列出关于x的方程,解方程求得x的值即可求得∠AOC和∠BOF的值.
试题解析:
(1)∵∠BOD=∠AOC=76°,
又∵OE平分∠BOD,
∴∠DOE=![]() ∠BOD=
∠BOD=![]() ×76°=38°.
×76°=38°.
∴∠COE=180°﹣∠DOE=180°﹣38°=142°,
∵OF平分∠COE,
∴∠EOF=![]() ∠COE=
∠COE=![]() ×142°=71°,
×142°=71°,
∴∠BOF=∠EOF﹣∠BOE=71°﹣38°=33°.
(2)∵OE平分∠BOD,OF平分∠COE,
∴∠BOE=∠EOD,∠COF=∠FOE,
∴设∠BOE=x,则∠DOE=x,
故∠COA=2x,∠EOF=∠COF=x+36°,
则∠AOC+∠COF+∠BOF=2x+x+36°+36°=180°,
解得:x=36°,
故∠AOC=72°.
(3)设∠BOE=x,
∵OE平分∠BOD,∠BOD=∠AOC,
∴∠DOE=x,∠COA=2x,
∴∠BOC=180°-2x,
∴∠COE=180°-x,
∵OF平分∠COE,
∴∠EOF=90°-![]() x,
x,
∴∠BOF=90°﹣![]() x,
x,
∵|∠AOC﹣∠BOF|=α°,
∴|2x﹣(90°﹣![]() x)|=α°,
x)|=α°,
解得:x=(![]() )°+
)°+![]() α°或x=(
α°或x=(![]() )°﹣
)°﹣![]() α°,
α°,
当x=(![]() )°+
)°+![]() α°时,
α°时,
∠AOC=2x=(![]() )°+
)°+![]() α°,
α°,
∠BOF=90°﹣![]() x=(
x=(![]() )°﹣
)°﹣![]() α°;
α°;
当x=(![]() )°﹣
)°﹣![]() α°时,
α°时,
∠AOC=2x=(![]() )°﹣
)°﹣![]() α°,
α°,
∠BOF=90°﹣![]() x=(
x=(![]() )°+
)°+![]() α°.
α°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在我国古代的房屋建筑中,窗棂是重要的组成部分,具有高度的艺术价值.下列窗棂的图案中,是中心对称图形但不是轴对称图形的是( )
A.
B.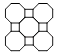
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°,求出图中阴影部分的面积.
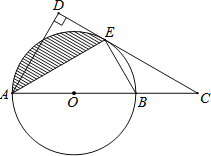
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D是AB的中点,过点D作DE⊥AC于点E, 延长DE到点F,使得EF=DE,连接AF,CF.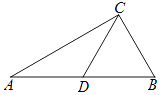
(1)根据题意,补全图形;
(2)求证:四边形ADCF是菱形;
(3)若AB=8,∠BAC=30°,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年6月17日北京国际自行车大会召开,来自世界各地的4000多名骑游爱好者齐聚夏都延庆.各种自行车赛事也带动了延庆的骑游产业.据调查,延庆区某骑游公司每月的租赁自行车数的增长率相同,今年四月份的骑游人数约为9000人,六月份的骑游人数约为16000人,求该骑游公司租赁自行车数的月平均增长率(精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,边AB、AC的中垂线交于点O,则有( )
A. O在△ABC内部 B. O在△ABC的外部
C. O在BC边上 D. OA=OB=OC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动中,共募得捐款32000000元,将32000000用科学记数法表示为
A.0.32×108B.3.2×106C.3.2×107D.32×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com