已知:如图.在中..点在上.以为圆心.长为半径的圆与分别交于点.且．(1)判断直线与的位置关系.并证明你的结论,(2)若.=.求的值．题目和参考答案——青夏教育精英家教网—

（本小题满分5分）已知：如图，在中，，点在上，以为圆心，长为半径的圆与分别交于点，且．
（1）判断直线与的位置关系，并证明你的结论；
（2）若，=，求的值．

．解：（1）直线与相切．------------------------------------------------------------------1分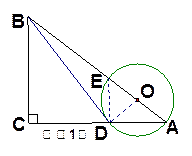

证明：如图1，连结．
，
∴．
，       ∴．
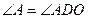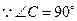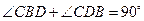又，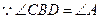
∴．
∴．
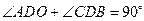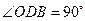∴直线与相切．    ---------------------------------------------------------------------------2分
（2）解法一：如图1，连结．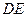
，，=
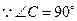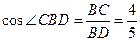∴． ---------------------------------------------------------------------------3分
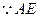是的直径，      ∴．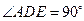
∴．
∵，
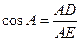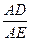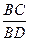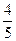∴==．----------------------------------------------------------------------------------------4分
∵AE=2AO
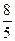∴=---------------------------------------------------------------------------------------------------5分
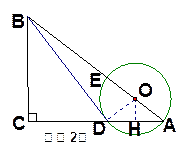
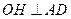解法二：如图2，过点作于点．
∴．
∴
，，=
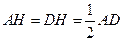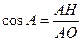
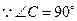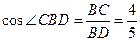∴．-------------------------------------------------------------------------- 3分
∵，
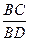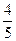∴==．-------------------------------------------------------------------------------------4分
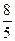∴=    -----------------------------------------------------------------------------------------5分

解析

练习册系列答案

世纪百通主体课堂小学课时同步达标系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

（本小题满分10分）

已知：如图，AD、BC是的两条弦，且．求证：．

查看答案和解析>>

科目：初中数学 来源： 题型：

（本小题满分9分）已知A、B两地的路程为240千米，某经销商每天都要用汽
车或火车将x吨保鲜品一次性由A地运往B地，受各种因素限制，下一周只能采用汽车和
火车中的一种进行运输，且须提前预订.。现在有货运收费项目及收费标准表，行驶路程S
（千米）与行驶时间t（时）的函数图象（如图13中①），上周货运量折线统计图（如图13
中②）等信息如下：

（1）汽车的速度为__________千米/时，火车的速度为_________千米/时；
（2）设每天用汽车和火车运输的总费用分别为y_汽（元）和y_火（元），分别求y_汽、y_火与x的函数关系式（不必写出x的取值范围）及x为何值时y_汽＞y_火；（总费用=运输费＋冷藏费＋固定费用）
（3）请你从平均数、折线图走势两个角度分析，建议该经销商应提前下周预定哪种运输工具，才能使每天的运输总费用较省？

查看答案和解析>>

科目：初中数学 来源： 题型：

（本小题满分5分）
已知直线