练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

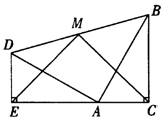
    两个全等的含300， 600角的三角板ADE和三角板ABC如图所示放置，E，A，C三点在一条直线上，连结BD，取BD的中点M，连结ME，MC。试判断△EMC的形状，并说明理由。

    解：△EMC是等腰直角三角形。

    证明：由题意，得

    DE=AC，∠DAE＋∠BAC=900，

    ∴∠DAB=900。

    连接AM．∵DM=MB

    ∴MA=DB=DM，∠MDA=∠MAB=450.

    ∴∠MDE=∠MAC=1050

    ∴△EDM≌△CAM

    ∴EM=MC， ∠DME=∠AMC

    又∠EMC=∠EMA+∠AMC=∠EMA+∠DME=900

    ∴CM⊥EM

    所以△EMC是等腰直角三角形

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：044

    两个全等的含30°, 60°角的三角板ADE和三角板ABC如图所示放置，E,A,C三点在一条直线上，连结BD，取BD的中点M，连结ME，MC．试判断△EMC的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年福建南安乐峰中学九年级上学期期末跟踪测试数学试卷（解析版） 题型：解答题

    如图所示，污水处理公司为某楼房建一座周长为30米的三级污水处理池，平面图为矩形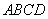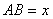，米，中间两条隔墙分别为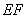、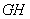，池墙的厚度不考虑．

    (1)用含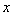的代数式表示外围墙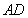的长度；

    (2)如果设计时要求矩形水池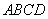恰好被隔墙分成三个全等的矩形，且它们均与矩形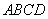相似，求此时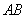的长；

    (3)如果设计时要求矩形水池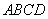恰好被隔墙分成三个全等的正方形.已知池的外围墙建造单价为每米400元，中间两条隔墙建造单价每米300元，池底建造的单价为每平方米100元.试计算此项工程的总造价.（结果精确到1元）

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

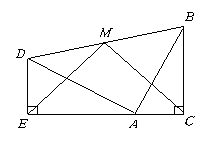
    两个全等的含300，600角的三角板ADE和三角板ABC如图所示放置，E，A，C三点在一条直线上，连结BD，取BD的中点M，连结ME，MC，试判断△EMC的形状，并说明理由。

     

    查看答案和解析>>

    同步练习册答案