
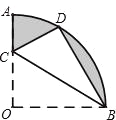
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,则有下列选项:
①∠ACD=60°;
②CB=6![]() ;
;
③阴影部分的周长为12+3π;
④阴影部分的面积为9π﹣12![]() .
.
其中正确的是 (填写编号).
【答案】①③④.
【解析】
试题分析:①正确.如图连接OD.
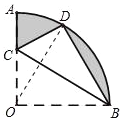
∵△BCD是由△BCO翻折得到,
∴BO=BD=OD,
∴△ODB是等边三角形,
∴∠DBO=60°,
∴∠CBO=∠CBD=30°,
∵∠COB=90°,
∴∠OCB=90°﹣∠CBO=60°=∠BCD,
∴∠ACD=180°﹣∠BCO﹣∠BCD=60°,故①正确.
②错误.在RT△BOC中,∵∠BOC=90°,OB=6,∠OBC=30°,
∴cos30°=![]() ,
,
∴BC=4![]() ,故②错误.
,故②错误.
③正确.阴影部分周长=AC+CD+BD+弧AB的长=AC+OC+BO+弧AB的长=12+![]() =12+3π,故③正确.
=12+3π,故③正确.
④正确.阴影部分面积=S扇形OAB﹣2S△BOC=![]() π62﹣2×
π62﹣2×![]() ×6×2
×6×2![]() =18π﹣12
=18π﹣12![]() ,故④正确.
,故④正确.
故答案为①③④.


科目:初中数学 来源: 题型:
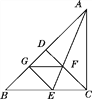
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于点F,交BC于点E,过点E作EG⊥AB于G,连结GF.求证:四边形CFGE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
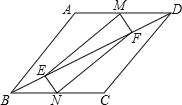
【题目】如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证:
(1)∠DFM=∠BEN;
(2)四边形MENF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△MNP中,∠N=60°,MN=3,NP=6,正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD沿边MN→NP进行翻滚,直到正方形有一个顶点与P重合即停止滚动,正方形在整个翻滚过程中,点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是( )
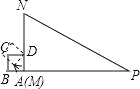
A.![]() +2 B.2π+2 C.
+2 B.2π+2 C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
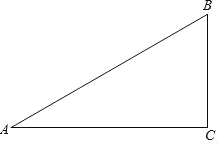
【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°.
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)连接DE,求证:△ADE≌△BDE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com