
【题目】综合与探究:
如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,其中
两点,其中![]() .
.

(1)求![]() 的值;
的值;
(2)若点![]() 是直线
是直线![]() 上的一个动点,当点
上的一个动点,当点![]() 仅在第一象限内运动时,试写出
仅在第一象限内运动时,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)探索:
①在(2)条件下,当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积是
的面积是![]() ;
;
②在①成立的情况下,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使△
,使△![]() 是等腰三角形?若存在,请写出满足条件的所有
是等腰三角形?若存在,请写出满足条件的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
【答案】(1)k=2;(2)S=x-1;(3)①当![]() 的坐标为
的坐标为![]() 时,
时,![]() 的面积是
的面积是![]() ;②存在,点
;②存在,点![]() 坐标P1(-2
坐标P1(-2![]() ,0),P2(2
,0),P2(2![]() ,0),P3(4,0),P4(2,0)..
,0),P3(4,0),P4(2,0)..
【解析】
(1)先确定出点B的坐标,代入函数解析式中即可求出k;
(2)借助(1)得出的函数关系式,利用三角形的面积公式即可求出函数关系式;
(3)①利用三角形的面积求出求出点A坐标;
(1)∵OB=1,
∴B(1,0),
∵点B在直线y=kx-2上,
∴k-2=0,
∴k=2
(2)由(1)知,k=2,
∴直线BC解析式为y=2x-2,
∵点A(x,y)是第一象限内的直线y=2x-2上的一个动点,
∴y=2x-2(x>1),
∴S=S△AOB=![]() ×OB×|yA|=
×OB×|yA|=![]() ×1×|2x-2|=x-1,
×1×|2x-2|=x-1,
(3)①如图,
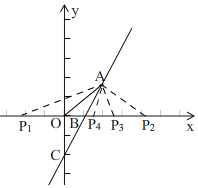
由(2)知,S=x-1,
∵△AOB的面积是1;
∴x=2,
∴A(2,2),
∴OA=2![]() ,
,
②设点P(m,0),
∵A(2,2),
∴OP=|m|,AP=![]() ,
,
①当OA=OP时,
∴2![]() =|m|,
=|m|,
∴m=±2![]() ,
,
∴P1(-2![]() ,0),P2(2
,0),P2(2![]() ,0),
,0),
②当OA=AP时,
∴2![]() =
=![]() ,
,
∴m=0或m=4,
∴P3(4,0),
③当OP=AP时,
∴|m|=![]() ,
,
∴m=2,
∴P4(2,0),
即:满足条件的所有P点的坐标为P1(-2![]() ,0),P2(2
,0),P2(2![]() ,0),P3(4,0),P4(2,0).
,0),P3(4,0),P4(2,0).


科目:初中数学 来源: 题型:
【题目】探究:数轴上任意两点之间的距离与这两点对应的数的关系.
![]()
(1)如果点A表示数5,将点A先向左移动4个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
如果点A表示数﹣2,将点A向右移动5个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
(2)发现:在数轴上,如果点M对应的数是m,点N对应的数是n,那么点M与点N之间的距离可表示为 (用m、n表示,且m≥n).
(3)应用:利用你发现的结论解决下列问题:数轴上表示x和﹣2的两点P与Q之间的距离是3,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
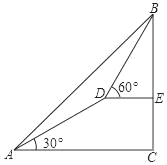
【题目】如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,求山的高度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=![]() AB.
AB.

探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=![]() AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣![]() ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
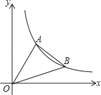
【题目】如图,直线y=![]() x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=
x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=![]() .
.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)求S△OAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b, A、B两点之间的距离表示为|AB|,利用数形结合思想回答下列问题:
![]()
(1)数轴上表示﹣3和1两点之间的距离是 ;
(2)数轴上表示x和﹣2的两点之间的距离表示为 ;
(3)若x表示一个有理数,且-3<x<1,则|x﹣1|+|x+3|的最小值是 ;
(4)若x表示一个有理数,且|x﹣1|+|x+3|>4,则有理数x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:![]() ,点
,点![]() ……在射线ON上,点
……在射线ON上,点![]() ……在射线OM上,△
……在射线OM上,△![]() 、△
、△![]() 、△
、△![]() ……均为等边三角形,若
……均为等边三角形,若![]() ,则△
,则△![]() 的边长为( )
的边长为( )

A. 6 B. 12 C. 32 D. 64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且![]() (无满分),将其按分数段分为五组,绘制出以下不完整表格:
(无满分),将其按分数段分为五组,绘制出以下不完整表格:

请根据表格提供的信息,解答以下问题:
(1)本次决赛共有________名学生参加;
(2)直接写出表中:a= ,b= 。
(3)请补全右面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com