
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 的图像交于点
的图像交于点![]() ,
,![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)结合函数图像,写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 的面积是
的面积是![]() 面积的3倍,请求出点
面积的3倍,请求出点![]() 的坐标.
的坐标.
【答案】(1)k1=-5,k2=-1;(2)x<-1或0<x<5;(3)P(0,16)或(0,-8)
【解析】
(1)把点A坐标代入![]() 即可求出k1的值,把点B的坐标代入反比例函数解析式即可求出m的值,最后把A、B的坐标都代入
即可求出k1的值,把点B的坐标代入反比例函数解析式即可求出m的值,最后把A、B的坐标都代入![]() 解方程组即可求出k2,b的值;
解方程组即可求出k2,b的值;
(2)观察图象直线![]() 的图象在反比例函数
的图象在反比例函数![]() 的图象的上方时,对应的自变量的取值范围就是不等式的解集;
的图象的上方时,对应的自变量的取值范围就是不等式的解集;
(3)设出P点坐标,根据![]() 的面积是
的面积是![]() 面积的3倍构建方程即可求出点P的坐标.
面积的3倍构建方程即可求出点P的坐标.
解:(1)∵A(-1,5)在反比例函数的图象上,
∴k1=-1×5=-5.
∴反比例函数解析式为![]() .
.
∵点B(m,-1)在反比例函数的图象上,
∴m=5.
把A(-1,5)、B(5,-1)代入![]() 得:
得:
 ,
,
解得:![]() ,
,
故k1=-5,k2=-1;
(2))∵A(-1,5)、B(5,-1)是直线![]() 与反比例函数
与反比例函数![]() 的交点,
的交点,
观察图象可知:x<-1或0<x<5时,![]() ;
;
(3)设P(0,n),
∵直线AB交y轴于(0,4),
∴![]() ,
,
解得m=16或-8,
∴P(0,16)或(0,-8).


科目:初中数学 来源: 题型:
【题目】(1)问题发现.
如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 、
、![]() 、
、![]() 均在同一直线上,连接
均在同一直线上,连接![]() .
.

①求证:![]() .
.
②求![]() 的度数.
的度数.
③线段![]() 、
、![]() 之间的数量关系为__________.
之间的数量关系为__________.
(2)拓展探究.
如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() .
.

①请判断![]() 的度数为____________.
的度数为____________.
②线段![]() 、
、![]() 、
、![]() 之间的数量关系为________.(直接写出结论,不需证明)
之间的数量关系为________.(直接写出结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )

A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B,C的坐标分别为(a,0),(2,﹣4),(c,0),且a,c满足方程![]() 为二元一次方程.
为二元一次方程.
(1)求A,C的坐标.
(2)若点D为y轴正半轴上的一个动点.
①如图1,∠AOD+∠ADO+∠DAO=180°,当AD∥BC时,∠ADO与∠ACB的平分线交于点P,求∠P的度数;
②如图2,连接BD,交x轴于点E.若S△ADE≤S△BCE成立.设动点D的坐标为(0,d),求d的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价-进价)
甲 | 乙 | |
进价(元/件) | 14 | 35 |
售价(元/件) | 20 | 43 |
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
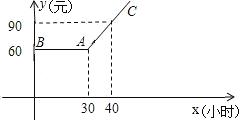
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com