
【题目】如图,已知□ABCD的对角线AC , BD交于点O , E , F分别是OA , OC的中点.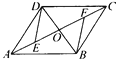
(1)求证:OE=OF;
(2)求证:DE∥BF .
【答案】
(1)
证明:∵ 四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是OA,OC的中点,
∴OE= OA,OF= OC,
∴OE=OF;
(2)
证明:∵在△DEO与△BFO中,
OE=OF,
∠BOE=∠DOF, BO=DO,
∴△BEO≌△DFO(SAS),
∴∠DEO=∠BFO,
∴DE∥BF.
【解析】(1)由平行四边形的性质得OA=OC , E , F分别是OA , OC的中点,可得OE=OF; (2)证△DOE≌△BOF , 得∠DEO=∠BFO , 得DE∥BF .
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】下列事件中,必然事件是( )
A. 在体育中考中,小明考了满分
B. 经过有交通信号灯的路口,遇到红灯
C. 抛掷两枚正方体骰子,点数和大于1
D. 四边形的外角和为180度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB , 当AD= , 平行四边形CDEB为菱形.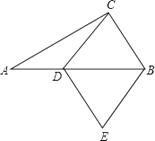
查看答案和解析>>
科目:初中数学 来源: 题型:
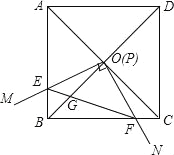
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OGBD=AE2+CF2.
;(5)OGBD=AE2+CF2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州东站位于城东新城天城路1号,总投资约250亿人民币,占地面积达113万平方米,其中1号、250亿、113万分别属于( )
A. 排序 计数 测量 B. 标号 计数 测量
C. 排序 计数 标号 D. 标号 计数 排序
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个利用四边形的不稳定性制作的菱形晾衣架.已知其中每个菱形的边长为20cm,墙上悬挂晾衣架的两个铁钉A、B之间的距离为 ![]() cm,则∠1等于( )
cm,则∠1等于( )
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com