
����Ŀ���ڻ������Ż�У�ij����С��Ҫ��һ�鿿ǽ��ǽ��25�ף��Ŀյ�����һ����������������������һ�߿�ǽ�������60m�������Χ���м���һ����ʵ�����������������ƽ����ǽ��һ��BC�ij�Ϊx��m���������������Ϊy��m2��
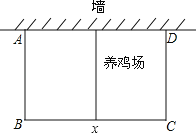
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2��������������ܴﵽ300m2�����ܣ������ʱx��ֵ�������ܣ�˵�����ɣ�
��3�����ݣ�1������õĺ�����ϵʽ���жϵ�xȡ��ֵʱ�����������������������Ƕ��٣�
���𰸡���1��y=x![]() ��60��x��=��
��60��x��=��![]() x2+20x��0��x��25������2�����ܣ�����������3����xȡ25mʱ������������������������
x2+20x��0��x��25������2�����ܣ�����������3����xȡ25mʱ������������������������![]() m2��
m2��
��������
�����������1������x��ʾ��AB�����ݾ��ε������ʽ�õ�y=��![]() x2+20x��Ȼ������ǽ��25�ɵõ�x��ȡֵ��Χ��
x2+20x��Ȼ������ǽ��25�ɵõ�x��ȡֵ��Χ��
��2����y=300�õ���![]() x2+20x=300�����x=30��Ȼ�����x��ȡֵ��Χ���ж���������������ܴﵽ300m2��
x2+20x=300�����x=30��Ȼ�����x��ȡֵ��Χ���ж���������������ܴﵽ300m2��
��3���ѣ�1���еĽ���ʽ��ɶ���ʽ��Ȼ�����ö��κ�����������⣮
�⣺��1��BC=x����AB=![]() ��60��x����
��60��x����
����y=x![]() ��60��x��=��
��60��x��=��![]() x2+20x��0��x��25����
x2+20x��0��x��25����
��2�����ܣ��������£�
��y=300ʱ������![]() x2+20x=300��
x2+20x=300��
������x2��60x+900=0�����x1=x2=30��
��Ϊ0��x��25��
����x=30������������
����������������ܴﵽ300m2��
��3��y=��![]() x2+20x=��
x2+20x=��![]() ��x��30��2+300��
��x��30��2+300��
��Ϊ0��x��25��
���Ե�x=25ʱ��y��ֵ������ֵΪ��![]() ��25��30��2+300=
��25��30��2+300=![]() ��
��
�𣺵�xȡ25mʱ������������������������![]() m2��
m2��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD��BC�ڵ�D��DΪBC���е㣬����AB����ABC��ƽ���߽�AD�ڵ�O������OC������AOC=130��������ABC= ��
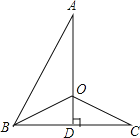
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P(1��1)��Q(1����1)������Q�̶�����P�Ƶ�Q��תʹ�߶�PQ��x�ᣬ���ʱ�ĵ�P��������_________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
��Ͱ���쳧��ij������Ҫ��������������Ͱ�õ�Բ����Ƭ�ͳ�������Ƭ���ó����й���42�ˣ�ÿ������ƽ��ÿСʱ��������Բ����Ƭ120Ƭ���߳�������Ƭ80Ƭ����ͼ��һ����Ͱ������Բ����Ƭ��һ����������Ƭ�����ף�����Բ����Ƭ�ͳ�������Ƭ�Ĺ��˸�Ϊ������ʱ������ʹ��������Ƭǡ�����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��һ�κ���ͼ����P(0��-3���� �Ҿ�����Q(2,3)
�����һ�κ�������ʽ��
��������X��Ľ��㡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڳ�����ABCD�У�AB=4��BC=![]() ��OΪBC��һ�㣬BO=
��OΪBC��һ�㣬BO=![]() ����ͼ��ʾ����BC����ֱ��Ϊx�ᣬOΪ����ԭ�㽨��ƽ��ֱ������ϵ��MΪ�߶�OC�ϵ�һ�㣮
����ͼ��ʾ����BC����ֱ��Ϊx�ᣬOΪ����ԭ�㽨��ƽ��ֱ������ϵ��MΪ�߶�OC�ϵ�һ�㣮
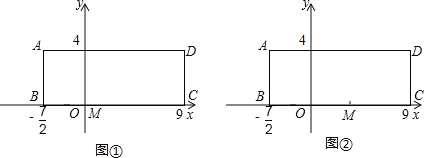
��1������M������Ϊ��1��0������ͼ�٣���OMΪһ����������OMP��ʹ��P��y���ϣ�����������ĵ����������м�������ֱ��д�����з��������ĵ�P�����ꣻ
��2������M������Ϊ��1��0������ͼ�٣���OMΪһ����������OMP��ʹ��P���ڳ�����ABCD��һ���ϣ�����������ĵ����������м�������ֱ��д�����з��������ĵ�P�����꣮
��3��������2���еĵ�M�������Ϊ��4��0���������������䣬��ͼ�ڣ���ô���������ĵ����������м�����������з��������ĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͳ������ȥ�깲��������500ǿ������ҵ19�ң��ۼ���������410000000��Ԫ������410000000�ÿ�ѧ��������ʾΪ�� ��
A��41��107 B��4.1��108 C��4.1��109 D��0.41��109
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A�������ϱ�ʾ+2���ӵ�A����������ƽ��3����λ����B�����B����ʾ��ʵ���ǣ� ��
A�� 3 B�� ��1 C�� 5 D�� ��1��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱ���ABC�У�D�DZ�AC��һ�㣬����BD������BCD�Ƶ�B��ʱ����ת60�㣬�õ���BAE������ED����BC=10��BD=9�������н��۴�����ǣ� ��
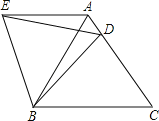
A��AE��BC
B����ADE���ܳ���19
C����BDE�ǵȱ�������
D����ADE=��BDC
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com