
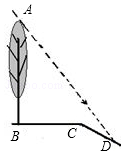
 如图,坡面CD的坡比为1:$\sqrt{3}$,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=$\sqrt{3}$米,求小树AB的高.
如图,坡面CD的坡比为1:$\sqrt{3}$,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=$\sqrt{3}$米,求小树AB的高. 分析 此题是把实际问题转化为解直角三角形问题,首先根据题意作图(如图),得Rt△AFD,Rt△CED,然后由Rt△CED,和坡面CD的坡比为1:$\sqrt{3}$,求出CE和ED,再由Rt△AFD和三角函数求出AF.进而求出AB.
解答 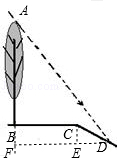 解:如图,过D作水平线DF,与AB的延长线交于F,过C作CE⊥DF于E,
解:如图,过D作水平线DF,与AB的延长线交于F,过C作CE⊥DF于E,
得:∠ADF=60°,FE=BC,BF=CE,
在Rt△CED中,设CE=x,由坡面CD的坡比为1:$\sqrt{3}$,得:DE=$\sqrt{3}$x,
则根据勾股定理得:
x2+( $\sqrt{3}$x)2=( $\sqrt{3}$)2,
得x=±$\frac{\sqrt{3}}{2}$,-$\frac{\sqrt{3}}{2}$不合题意舍去,
所以,CE=$\frac{\sqrt{3}}{2}$米,则ED=$\frac{3}{2}$米,
那么,FD=FE+ED=BC+ED=3+$\frac{3}{2}$=$\frac{9}{2}$米,
在Rt△AFD中,由三角函数得:
$\frac{AF}{FD}$=tan∠ADF,
∴AF=FD•tan60°=$\frac{9}{2}$×$\sqrt{3}$=$\frac{9\sqrt{3}}{2}$米,
∴AB=AF-BF=AF-CE=$\frac{9\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$=4 $\sqrt{3}$米,
答:小树AB的高为4$\sqrt{3}$米.
点评 此题考查的知识点是解直角三角形的应用-坡度坡角问题,解题的关键是把实际问题转化为解直角三角形问题,由Rt△AFD,Rt△CED求出AB.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com