
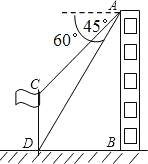
【题目】在20m高的楼AB的前方有一个旗杆CD,从楼的顶端A测得旗杆的顶端C的俯角为45°,底端D的俯角为60°.
(1)求旗杆的底端D与楼的底端B的距离;
(2)求旗杆CD的高度.
[说明:(1)(2)的计算结果精确到0.01m.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732].
≈1.732].
【答案】(1)旗杆的底端D与楼的底端B的距离约为11.55m;(2)旗杆CD的高度约为8.45m.
【解析】
试题分析:(1)在Rt△ABD中,利用AB的长和∠DAB的度数求得DB的值即为旗杆的底端D与楼的底端B的距离;
(2)作CE⊥AB与E点,利用两平行线之间的距离相等得到CE=DB,在直角三角形ACE中求得AE后,用AB减去AE即可得到旗杆的高度.
试题解析:(1)由题意可知,∠DAB=30°,
在Rt△ADB中,DB=ABtan30°,
=20×![]() ,
,
≈20×![]() ,
,
≈11.55,
答:旗杆的底端D与楼的底端B的距离约为11.55m;
(2)作CE⊥AB,垂足为E,

则四边形CDBE为矩形.
∴CE=DB,CD=EB,
在Rt△ACE中,∠CAE=45°,AE=CE=DB=![]() ,
,
∴CD=EB=AB-AE,
=20-![]() ≈20-
≈20-![]() ,
,
≈8.45.
答:旗杆CD的高度约为8.45m.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
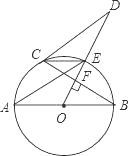
【题目】如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 过一点有且只有一条直线与已知直线垂直
B. 三角形任意两边之和小于第三边
C. 三角形的一个外角大于它的任何一个内角
D. 平行与同一条直线的两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.某中学为了解学生体育活动情况,随机抽查了520名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,并根据调查结果绘制成如下不完整的统计图.
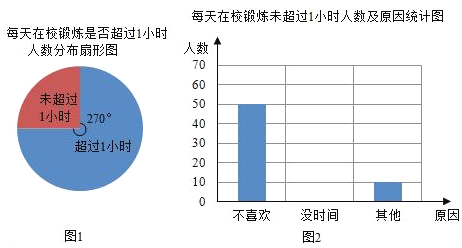
根据统计图提供的信息,解答下列问题:
(1)这520名毕业生中每天在校锻炼时间超过1消失的人数是 .
(2)请补全条形统计图.
(3)2016年该中学所在城市的初中毕业生约为5.2万人,估计2016年该城市初中毕业生中因为没时间导致每天锻炼时间未超过1小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
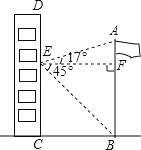
【题目】如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).
【参考数据:sin17°=0.29,cos17°=0.96,tan17°=0.31】
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com