练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．反比例函数y=$\frac{k-1}{x}$的图象经过A（x1，y1），B（x2，y2）两点，其中x1＜x2＜0，且y1＞y2，则k的范围是k＞1．

    分析 由中x1＜x2＜0，且y1＞y2，得出在同一象限内y随x的增大而减小解答即可．

    解答 解：∵反比例函数y=$\frac{k-1}{x}$的图象经过A（x1，y1），B（x2，y2）两点，其中x1＜x2＜0，且y1＞y2，
    ∴在同一象限内y随x的增大而减小，
    ∴k-1＞0，即k＞1．
    故答案为：k＞1．

    点评 本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．如图，埃航MS804客机失事后，国家主席亲自发电进行慰问，埃及政府出动了多艘舰船和飞机进行搜救，其中一艘潜艇在海面下500米的A点处测得俯角为45°的前下方海底有黑匣子信号发出，继续沿原方向直线航行2000米后到达B点，在B处测得俯角为60°的前下方海底有黑匣子信号发出，求海底黑匣子C点距离海面的深度（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，在菱形ABCD中，点E、F分别是BD、CD的中点，EF=6cm，则菱形ABCD的周长是（　　）
    A．12cmB．48cmC．30cmD．24cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某书店准备购进甲、乙两种图书共100本，购书款不高于2224元，预这100本图书全部售完的利润不低于1100元，两种图书的进价、售价如表所示：
      甲种图书 乙种图书
     进价（元/本） 16 28
     售价（元/本） 26 40
    请回答下列问题：
    （1）书店有多少种进书方案？
    （2）在这批图书全部售出的条件下，（1）中的哪种方案利润最大？最大利润是多少？（请你用所学的函数知识来解决）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．小红、小明在玩“剪子、包袱、锤子”游戏，小红给自己一个规定：一直不出“锤子”．小红、小明获胜的概率分别是P1，P2，则下列结论正确的是（　　）
    A．P1=P2B．P1＞P2C．P1＜P2D．P1≤P2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

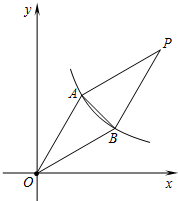    9．已知：如图，双曲线y=$\frac{k}{x}$在第一象限的分支经过A、B两点，点A的坐标为（2，2$\sqrt{3}$），点B的坐标为（m，2）．
    （1）求k和m值；
    （2）求∠AOB的度数；
    （3）将△ABO沿着AB翻折得到△ABP，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．在一个密闭不透明的袋子里有若干个白球．为估计白球个数，小何向其中投入8个黑球，搅拌均匀后随机摸出一个球，记下颜色，再把它放入袋中，不断重复摸球400次，其中88次摸到黑球，则估计袋中大约有白球（　　）
    A．18个B．28个C．36个D．42个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．在一个不透明的口袋里装有四个小球，球面上分别标有数字-2、0、1、2，它们除数字不同外没有任何区别，每次实验先搅拌均匀．
    （1）从中任取一球，求抽取的数字为负数的概率；
    （2）从中任取一球，将球上的数字记为x（不放回）；再任取一球，将球上的数字记为y，试用画树状图（或列表法）表示所有可能出现的结果，并求“x+y＞0”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

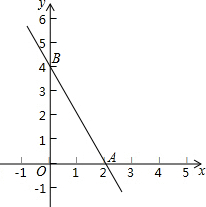    14．如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2，b1≠b2，那么称这两个一次函数为“平行一次函数”．
    如图，已知函数y=-2x+4的图象与x轴、y轴分别交于A、B两点，一次函数y=kx+b与y=-2x+4是“平行一次函数”
    （1）若函数y=kx+b的图象过点（3，1），求b的值；
    （2）若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形，位似中心为原点，位似比为1：2，求函数y=kx+b的表达式．

    查看答案和解析>>

    同步练习册答案