
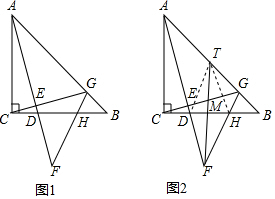
分析 (1)结论:FH=FD.只要证明∠5=∠6即可;
(2)作BK⊥BC交CG的延长线于K.由△BGK≌△GBH,可得BH=BK,易证△ACD≌△CBK,可得CD=BK=BH,由(1)可知,四边形DFHT是菱形,
∴TF与DH相互平分,设交点为J,由JF∥AC,可得$\frac{JF}{AC}$=$\frac{DJ}{CD}$=$\frac{1}{2}$,设DJ=a,则CD=2a,AC=6a,JF=3a,DF=TH=$\sqrt{10}$a,由△CDF∽△ADC,可得$\frac{CD}{AD}$=$\frac{DE}{CD}$=$\frac{CE}{AC}$,推出DE=$\frac{\sqrt{10}}{5}$a,CE=$\frac{3\sqrt{10}}{5}$a,由CD=DH,DE∥HM,推出CE=EM,HM=2DE=$\frac{2\sqrt{10}}{5}$a,推出TM=TH-HM=$\frac{3\sqrt{10}}{5}$a,由DE∥TM,可得$\frac{EN}{MN}$=$\frac{DE}{TM}$=$\frac{\frac{\sqrt{10}}{5}a}{\frac{3\sqrt{10}}{5}a}$=$\frac{1}{3}$;
解答 解:(1)结论:FH=FD.
理由:∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵CE⊥AD,
∴∠3+∠CAE=90°,∠4+∠CAE=90°,
∴∠3=∠4=∠6,
∵∠1+∠3+∠CAG=180°,∠2+∠7+∠HBG=180°,
∵∠1=∠2,∴∠3=∠7=∠5,
∴∠5=∠6,
∴FH=FD.
(2)作BK⊥BC交CG的延长线于K.
∵∠BGK=∠BGH,BG=BG,∠GBK=∠GBH,
∴△BGK≌△GBH,
∴BH=BK,
易证△ACD≌△CBK,可得CD=BK=BH,
由(1)可知,四边形DFHT是菱形,
∴TF与DH相互平分,设交点为J,
∴JT=JF=JD=JH,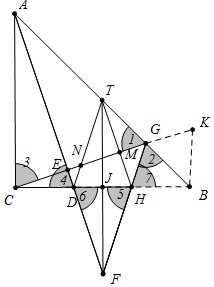
∴JC=JB,
∴JT=$\frac{1}{2}$AC,
∵JF∥AC,
∴$\frac{JF}{AC}$=$\frac{DJ}{CD}$=$\frac{1}{2}$,设DJ=a,则CD=2a,AC=6a,JF=3a,DF=TH=$\sqrt{10}$a,
由△CDF∽△ADC,
∴$\frac{CD}{AD}$=$\frac{DE}{CD}$=$\frac{CE}{AC}$,
∴DE=$\frac{\sqrt{10}}{5}$a,CE=$\frac{3\sqrt{10}}{5}$a,
∵CD=DH,DE∥HM,
∴CE=EM,HM=2DE=$\frac{2\sqrt{10}}{5}$a,
∴TM=TH-HM=$\frac{3\sqrt{10}}{5}$a,
∵DE∥TM,
∴$\frac{EN}{MN}$=$\frac{DE}{TM}$=$\frac{\frac{\sqrt{10}}{5}a}{\frac{3\sqrt{10}}{5}a}$=$\frac{1}{3}$,
点评 本题考查翻折变换、等腰直角三角形的性质、全等三角形的判定和性质、平行线分线段成比例定理、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题.


科目:初中数学 来源: 题型:选择题
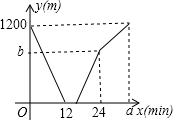 甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:
甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:| A. | ①② | B. | ①②③ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com