
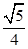 x2+
x2+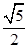 x或y=
x或y=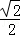 x2+
x2+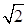 x.
x.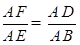 =
=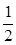 ,即AE=2AF②,①与②联立组成二元一次方程组,解出AE=2,AF=1,进而得到点A的坐标;
,即AE=2AF②,①与②联立组成二元一次方程组,解出AE=2,AF=1,进而得到点A的坐标;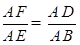 =
=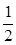 ,即AE=2AF②,
,即AE=2AF②,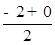 =﹣1,
=﹣1,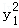 =36,解得y1=±2
=36,解得y1=±2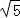 (负值舍去).
(负值舍去).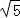 )代入y=ax2+bx,
)代入y=ax2+bx,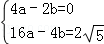 ,解得
,解得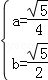 .
.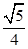 x2+
x2+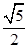 x;
x;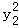 =36,解得y2=±4
=36,解得y2=±4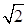 (负值舍去).
(负值舍去).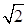 )代入y=ax2+bx,
)代入y=ax2+bx, ,解得
,解得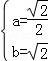 .
.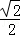 x2+
x2+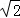 x.
x.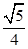 x2+
x2+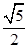 x或y=
x或y=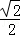 x2+
x2+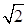 x.
x.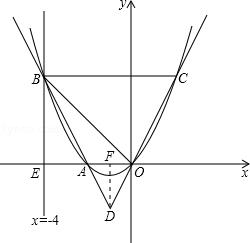


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
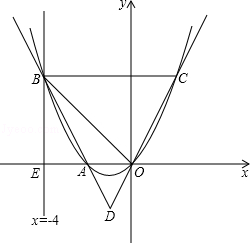
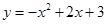 交
交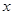 轴于
轴于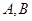 两点(
两点( 的左侧),交
的左侧),交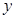 轴于点
轴于点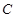 ,顶点为
,顶点为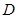 。
。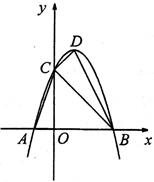
 的坐标;
的坐标;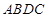 的面积;
的面积;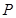 ,使得
,使得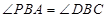 ,若存在,请求出点
,若存在,请求出点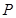 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
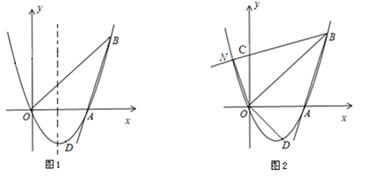
 的图像经过原点及点A(1,2),与x轴相交于另一点B.
的图像经过原点及点A(1,2),与x轴相交于另一点B.
 的解析式及B点坐标;
的解析式及B点坐标; 以
以 为对称轴向右翻折后,得到一个新的二次函数
为对称轴向右翻折后,得到一个新的二次函数 ,已知二次函数
,已知二次函数 与x轴交于两点,其中右边的交点为C点.点P在线段OC上,从O点出发向C点运动,过P点作x轴的垂线,交直线AO于D点,以PD为边在PD的右侧作正方形PDEF(当P点运动时,点D.点E、点F也随之运动);
与x轴交于两点,其中右边的交点为C点.点P在线段OC上,从O点出发向C点运动,过P点作x轴的垂线,交直线AO于D点,以PD为边在PD的右侧作正方形PDEF(当P点运动时,点D.点E、点F也随之运动);查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com