
分析 设$\frac{x}{y+z+u}$=$\frac{y}{z+u+x}$=$\frac{z}{u+x+y}$=$\frac{u}{x+y+z}$=$\frac{1}{t}$,可得y+z+u=tx,z+u+x=ty,u+x+y=tz,x+y+z=tu,四式相加得:3(x+y+z+u)=t(x+y+z+u),分两种情况当x+y+z+u=0时,当x+y+z+u≠0时,t=3时分别求解即可.
解答 解:设$\frac{x}{y+z+u}$=$\frac{y}{z+u+x}$=$\frac{z}{u+x+y}$=$\frac{u}{x+y+z}$=$\frac{1}{t}$,
∴y+z+u=tx,z+u+x=ty,u+x+y=tz,x+y+z=tu,
四式相加得:3(x+y+z+u)=t(x+y+z+u),
当x+y+z+u=0时,$\frac{x+y}{z+u}$+$\frac{y+z}{u+x}$+$\frac{z+u}{x+y}$+$\frac{u+x}{y+z}$=$\frac{-(z+u)}{z+u}$+$\frac{-(u+x)}{u+x}$+$\frac{-(x+y)}{x+y}$+$\frac{-(y+z)}{y+z}$=-4,
当x+y+z+u≠0时,t=3,
∴y+z+u=3x,z+u+x=3y,u+x+y=3z,x+y+z=3u,
前两个式子相减得y-x=3(x-y),得x=y,
同理可得y=z,z=u,u=x,
∴x=y=z=u,
∴$\frac{x+y}{z+u}$+$\frac{y+z}{u+x}$+$\frac{z+u}{x+y}$+$\frac{u+x}{y+z}$=4,
综上所述:$\frac{x+y}{z+u}$+$\frac{y+z}{u+x}$+$\frac{z+u}{x+y}$+$\frac{u+x}{y+z}$=4或-4.
点评 本题主要考查了分式的化简求值,解题的关键是设$\frac{x}{y+z+u}$=$\frac{y}{z+u+x}$=$\frac{z}{u+x+y}$=$\frac{u}{x+y+z}$=$\frac{1}{t}$,分两种情况求解.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
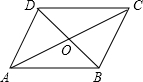 如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )
如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )| A. | 1<m<11 | B. | 2<m<22 | C. | 10<m<12 | D. | 5<m<6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com