
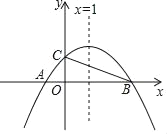
【题目】如图,已知抛物线y=ax2+bx+1与x轴相交于点A,B,与y轴相交于点C,点A的坐标为(﹣1,0),对称轴为直线x=1.
(1)求点B的坐标及抛物线的解析式;
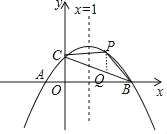
(2)在直线BC上方的抛物线上有一点P,使△PBC的面积为1,求出点P的坐标.
【答案】(1)点B的坐标为:B(3,0),抛物线解析式为y=﹣![]() x2+
x2+![]() x+1;(2)P点坐标为(1,
x+1;(2)P点坐标为(1,![]() )或(2,1).
)或(2,1).
【解析】
(1)利用抛物线的对称性确定B(3,0),然后利用交点式求抛物线解析式;
(2)作PQ∥y轴于Q,如图,利用待定系数法求出直线BC的解析式为y=![]() x+1,设P(t,
x+1,设P(t,![]() t2+
t2+![]() t +1)(0<t<3),则Q(t,
t +1)(0<t<3),则Q(t,![]() t+1),则PQ=
t+1),则PQ=![]() t2+t,利用三角形面积公式得到
t2+t,利用三角形面积公式得到![]() ×3×(
×3×(![]() t2+t)=1,然后解方程求出t即可得到P点坐标.
t2+t)=1,然后解方程求出t即可得到P点坐标.
解:(1)∵点A的坐标为(﹣1,0),对称轴为直线x=1,
∴B(3,0),
设抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∵﹣3a=1,
∴a=![]() ,
,
∴抛物线解析式为y=![]() x2+
x2+![]() x+1;
x+1;
(2)作PQ∥y轴于Q,如图,
当x=0时,y=![]() x2+
x2+![]() x+1=1,则C(0,1)
x+1=1,则C(0,1)
设直线BC的解析式为y=mx+n,
把C(0,1),B(3,0)代入得![]() ,解得
,解得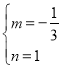 ,
,
∴直线BC的解析式为y=![]() x+1,
x+1,
设P(t,![]() t2+
t2+![]() t+1)(0<t<3),则Q(t,
t+1)(0<t<3),则Q(t,![]() t+1)
t+1)
∴PQ=![]() t2+
t2+![]() t+1﹣(
t+1﹣(![]() t+1)=
t+1)=![]() t2+t,
t2+t,
∵△PBC的面积为1,
∴![]() ×3×(
×3×(![]() t2+t)=1,
t2+t)=1,
整理得t2﹣3t+2=0,解得t1=1,t2=2,
∴P点坐标为(1,![]() )或(2,1).
)或(2,1).
故答案为:(1)点B的坐标为:B(3,0),抛物线解析式为y=﹣![]() x2+
x2+![]() x+1;(2)P点坐标为(1,
x+1;(2)P点坐标为(1,![]() )或(2,1).
)或(2,1).


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
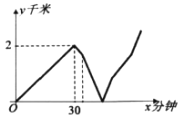
【题目】周末小明匀速步行赶往学校参加学校组织的植树活动,小明从家出发30分钟后,忽然想起没有带植树工具,于是马上掉头往回走行走速度比之前提高了1千米/时(仍保持匀速步行),同时小明打电话给爸爸,请爸爸帮他把植树工具送过来,从小明开始打电话到爸爸出门一共用了4分钟,爸爸的行走速度与此时小明的行走速度相同,两人相遇后,小明立即赶往学校,爸爸则转身回家,两人速度均保持不变,爸爸在回家途中用了10分钟吃早餐,然后立即回家,当爸爸到家时小明刚好到达学校.爸爸和小明相距的路程y(千米)与小明从家出发的时间x(分钟)之间的关系如图所示,求今天早上小明从家到学校途中行走的总路程是________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《![]() 年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分
年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分![]() 分),社区管理员随机从有
分),社区管理员随机从有![]() 人的某小区抽取若干名人员的答卷成绩,并对他们的成绩(单位:分)统计整理后绘制了一幅不完整的统计表(如图所示)
人的某小区抽取若干名人员的答卷成绩,并对他们的成绩(单位:分)统计整理后绘制了一幅不完整的统计表(如图所示)
等级 | 成绩( | 频数 | 频率 |
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
合计 |
|
| |
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() =___,
=___,![]() =_____;
=_____;
(2)根据抽样调查结果,请估计该小区答题成绩为“![]() 级”的有多少人?
级”的有多少人?
(3)该社区有![]() 名男管理员和
名男管理员和![]() 名女管理员,现从中随机挑选
名女管理员,现从中随机挑选![]() 名管理员参加“社区防控”宣传活动,请用树状图法或列表法求出恰好选中“
名管理员参加“社区防控”宣传活动,请用树状图法或列表法求出恰好选中“![]() 男
男![]() 女”的概率.
女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难,八方支援. 在湖北武汉新冠肺炎疫情爆发期间,我市甲、乙两所医院分别有一男一女共4名医护人员参与了支援湖北武汉抗击疫情的任务.
(1)若从甲、乙两医院的援鄂医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从援鄂的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
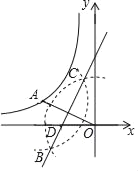
【题目】如图,点A在反比例函数![]() (x<0)的图象上,连接OA,分别以点O和点A为圆心,大于
(x<0)的图象上,连接OA,分别以点O和点A为圆心,大于![]() 的长为半径作弧,两弧相交于B,C两点,过B,C两点作直线交x轴于点D,连接AD.若∠AOD=30°,△AOD的面积为2,则k的值为( )
的长为半径作弧,两弧相交于B,C两点,过B,C两点作直线交x轴于点D,连接AD.若∠AOD=30°,△AOD的面积为2,则k的值为( )
A.﹣6B.6C.﹣2D.﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
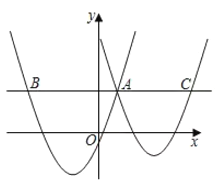
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 交于点A.过点A作
交于点A.过点A作![]() 轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为____.
轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点![]() 和
和![]() ,给出如下定义:
,给出如下定义:
如果 ,那么称点
,那么称点![]() 为点
为点![]() 的“伴随点”.
的“伴随点”.
例如:点![]() 的“伴随点”为点
的“伴随点”为点![]() ;点
;点![]() 的“伴随点”为点
的“伴随点”为点![]() .
.
(1)直接写出点![]() 的“伴随点”
的“伴随点”![]() 的坐标.
的坐标.
(2)点![]() 在函数
在函数![]() 的图象上,若其“伴随点”
的图象上,若其“伴随点”![]() 的纵坐标为2,求函数
的纵坐标为2,求函数![]() 的解析式.
的解析式.
(3)点![]() 在函数
在函数![]() 的图象上,且点
的图象上,且点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 的“伴随点”为
的“伴随点”为![]() .若点
.若点![]() 在第一象限,且
在第一象限,且![]() ,求此时“伴随点”
,求此时“伴随点”![]() 的横坐标.
的横坐标.
(4)点![]() 在函数
在函数![]() 的图象上,若其“伴随点”
的图象上,若其“伴随点”![]() 的纵坐标
的纵坐标![]() 的最大值为
的最大值为![]() ,直接写出实数
,直接写出实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(-2,a),C(3a-10,1)是反比例函数![]() (x<0)图象上的两点.
(x<0)图象上的两点.
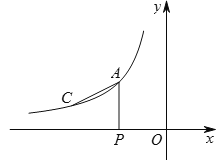
(1)求m的值;
(2)过点A作AP⊥x轴于点P,若直线y=kx+b经过点A,且与x轴交于点B,当∠PAC=∠PAB时,求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是一名健步走运动的爱好者,他用手机软件记录了他近期健步走的步数(单位:万步),绘制出如下的统计图①和统计图②,请根据相关信息,解答下列问题:
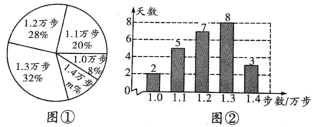
(Ⅰ)本次记录的总天数为_____________,图①中m的值为______________;
(Ⅱ)求小名近期健步走步数的平均数、众数和中位数;
(Ⅲ)根据样本数据,若小明坚持健步走一年(记为365天),试估计步数为1.1万步的天数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com