
 如图,在平行四边形ABCD中,AB=8,AD=6,∠DAB=30°,E、F是对角线AC的三等分点,则△BEF的面积是4.
如图,在平行四边形ABCD中,AB=8,AD=6,∠DAB=30°,E、F是对角线AC的三等分点,则△BEF的面积是4. 分析 作DM⊥AB于M,则∠AMD=90°,先求出DM=$\frac{1}{2}$AD=3,求出平行四边形ABCD的面积,得出△ABC的面积,得出△BEF的面积=$\frac{1}{3}$△ABC的面积.
解答 解:作DM⊥AB于E,如图所示: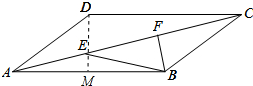 则∠AMD=90°,
则∠AMD=90°,
∵∠DAB=30°,
∴DM=$\frac{1}{2}$AD=3,
∴平行四边形ABCD的面积=AB•DM=8×3=24,
∴△ABC的面积=$\frac{1}{2}$平行四边形ABCD的面积=12,
∵E、F是对角线AC的三等分点,
∴AE=EF=CF,
∴△BEF的面积=$\frac{1}{3}$△ABC的面积=$\frac{1}{3}$×12=4;
故答案为:4.
点评 本题考查了平行四边形的性质、平行四边形面积的计算方法、三角形面积的计算;熟练掌握平行四边形的性质,运用含30°角的直角三角形的性质求出高是解决问题的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:选择题
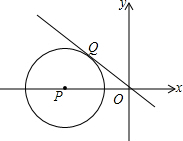 如图,⊙P是圆心P(-$\sqrt{2}$,0),正比例函数y=-x的图象与⊙P相切于点Q,则Q点的坐标为( )
如图,⊙P是圆心P(-$\sqrt{2}$,0),正比例函数y=-x的图象与⊙P相切于点Q,则Q点的坐标为( )| A. | (-1,1) | B. | ($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.636×106亿元 | B. | 6.36×106亿元 | C. | 6.36×105亿元 | D. | 63.6×104亿元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9×1011 | B. | 9×103 | C. | 90×1010 | D. | 0.9×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
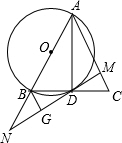 如图,已知在△ABC中,AD是BC边上的中线,以AB为直径的⊙O交BC于点D,过D作MN⊥AC于点M,交AB的延长线于点N,过点B作BG⊥MN于G.
如图,已知在△ABC中,AD是BC边上的中线,以AB为直径的⊙O交BC于点D,过D作MN⊥AC于点M,交AB的延长线于点N,过点B作BG⊥MN于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com