
【题目】如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B 
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为3cm,求 ![]() 的长度(结果保留π)
的长度(结果保留π)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.

(1)求证:G为CD的中点.
(2) 若CF=2,AE=3,求BE的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y= ![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y= ![]() (x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当 ![]() x+b<
x+b< ![]() 时,请直接写出x的取值范围.
时,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图. 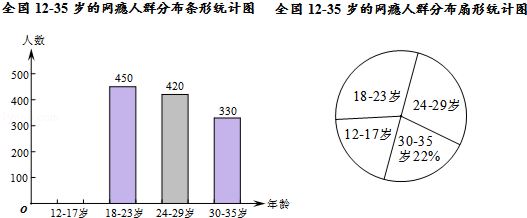
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
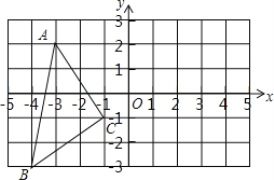
(1)在图中作出△ABC关于y轴对称的△A1B1C1;写出点△A1,B1,C1的坐标(直接写答案):A1 ;B1 ;C1 ;
(2)△A1B1C1的面积为 ;
(3)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,E、F、G、H分别是AB、BC、CD、DA边上的动点(不含端点),且EG、FH均过正方形的中心O.
(1)填空:OHOF (“>”、“<”、“=”);
(2)当四边形EFGH为矩形时,请问线段AE与AH应满足什么数量关系;
(3)当四边形EFGH为正方形时,AO与EH交于点P,求OP2+PHPE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B在坐标轴上,其中A(0,a)、B(b,0)满足:|2a﹣b﹣1|+![]() =0.
=0.
(1)求A、B两点的坐标;
(2)将线段AB平移到CD,点A的对应点为C(﹣2,t),如图1所示.若三角形ABC的面积为9,求点D的坐标;
(3)平移线段AB到CD,若点C、D也在坐标轴上,如图2所示,P为线段AB上的一动点(不与A、B重合),连接OP,PE平分∠OPB,∠BCE=2∠ECD.求证:∠BCD=3(∠CEP﹣∠OPE).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com