
 ≈1.732).
≈1.732).
 AD,以及PA=AD•cos30°进而得出DM的长,利用HM=DM•tan30°得出即可.
AD,以及PA=AD•cos30°进而得出DM的长,利用HM=DM•tan30°得出即可. BD=15,
BD=15, ,
, -1)≈11.0;
-1)≈11.0;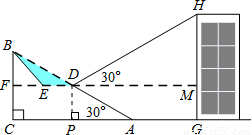
 AD=
AD= ×30=15,
×30=15, ×30=15
×30=15 .
. +27,
+27, ×(15
×(15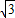 +27)=15+9
+27)=15+9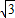 .
.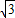 ≈45.6.
≈45.6.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
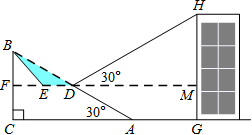
 如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(下面两小题的结果都精确到0.1米,参考数据:
如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(下面两小题的结果都精确到0.1米,参考数据:| 3 |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏苏州卷)数学(带解析) 题型:解答题
如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(请将下面2小题的结果都精确到0.1米,参考数据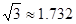 ).
).
【小题1】若修建的斜坡BE的坡角(即∠BAC)不大于45°,则平台DE的长最多为 ▲ 米;
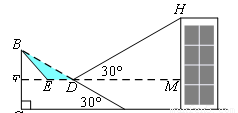
【小题2】一座建筑物GH距离坡脚A点27米远(即AG=27米),小明在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面上,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?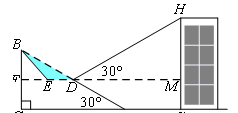
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江宁波城区五校联考初三第一学期12月月考数学试卷(解析版) 题型:解答题
如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
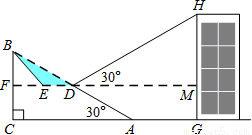
(1)若修建的斜坡BE的坡角(即∠BEF)不大于45°,则平台DE的长最多为多少米?
(2)一座建筑物GH距离坡角A点27米远(即AG=27米),小明在D点测得建筑物顶部H的仰角(即∠DHM)为30°,点B、C、A、G、H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:解答题
如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(请将下面2小题的结果都精确到0.1米,参考数据 ).
).
1.若修建的斜坡BE的坡角(即∠BAC)不大于45°,则平台DE的长最多为 ▲ 米;
2.一座建筑物GH距离坡脚A点27米远(即AG=27米),小明在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面上,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com