
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4),
(1)将△ABC各顶点的横坐标保持不变,纵坐标分别减5后得到△A1B1C1;
①请在图中画出△A1B1C1;
②求这个变换过程中线段AC所扫过的区域面积;
(2)将△ABC绕点(1,0)按逆时针方向旋转90°后得到的△A2B2C2,请在图中画出△A2B2C2,并分别写出△A2B2C2的顶点坐标.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
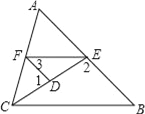
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
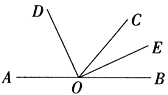
【题目】如图,O是直线AB上一点,OC是任意一条射线,OD,OE分别是∠AOC和∠BOC的平分线,
(1)图中∠BOD的补角是_______________;∠BOE的余角是____________________.
(2)如果∠BOE=![]() ∠AOD, 求∠BOE的度数。
∠AOD, 求∠BOE的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=3x的图象与反比例函数y= ![]() 的图象交于点A(1,m)和点B.
的图象交于点A(1,m)和点B. 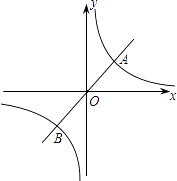
(1)求m的值和反比例函数的解析式.
(2)观察图象,直接写出使正比例函数的值大于反比例函数的值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红做了一个实验,将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置,所转过的度数是( ) 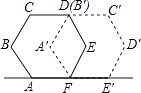
A.60°
B.72°
C.108°
D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表反映了x与y之间存在某种函数关系,现给出了几种可能的函数关系式: y=x+7,y=x﹣5,y=﹣ ![]() ,y=
,y= ![]() x﹣1
x﹣1
x | … | ﹣6 | ﹣5 | 3 | 4 | … |
y | … | 1 | 1.2 | ﹣2 | ﹣1.5 | … |
(1)从所给出的几个式子中选出一个你认为满足上表要求的函数表达式:;
(2)请说明你选择这个函数表达式的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∵DE∥BC(已知),∴∠1=____(____),∠2=_______(_____)又∵∠1=∠2(已知),∴∠B=∠C(____),∵∠3=∠B(已知),∴∠3=∠C(_________),∴DF∥AC(______)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在本校九年级学生中以“你最喜欢的一项体育运动”为主题进行了抽样调查,并将调查结果绘制成如图图表:
项目 | 篮球 | 乒乓球 | 羽毛球 | 跳绳 | 其他 |
人数 | a | 12 | 10 | 5 | 8 |
请根据图表中的信息完成下列各题: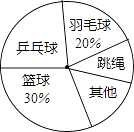
(1)本次共调查学生名;
(2)a= , 表格中五个数据的中位数是;
(3)在扇形图中,“跳绳”对应的扇形圆心角是;
(4)如果该年级有450名学生,那么据此估计大约有人最喜欢“乒乓球”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上. 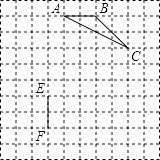
(1)填空:tanA= , AC=(结果保留根号);
(2)请你在图中找出一点D(仅一个点即可),连接DE、DF,使以D、E、F为顶点的三角形与△ABC全等,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com