
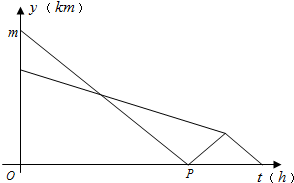
 某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.
某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.分析 (1)根据题意可以得到点m的值和点P的坐标,本题得以解决;
(2)根据题意可以得到各段对应的函数解析式,从而可以解答本题;
(3)根据题意可以得到先遣分队在相应的时间内所走的路程,从而可以得到先遣分队的步行速度;
(4)由题意可得到先遣分队先出发的路程,从而可以先遣分队比大部队早出发多少小时.
解答 解:(1)由题意可得,
图中m的值是90,点P的坐标是(1,0),
故答案为:90,(1,0);
(2)当0≤t≤1时,设y=kt+b,
则$\left\{\begin{array}{l}{b=90}\\{k+b=0}\end{array}\right.$
解得,$\left\{\begin{array}{l}{k=-90}\\{b=90}\end{array}\right.$
即当0≤t≤1时,y=-90t+90;
当1<t≤$\frac{4}{3}$时,设y=ct+d,
则$\left\{\begin{array}{l}{c+d=0}\\{\frac{4}{3}c+d=90×\frac{1}{3}}\end{array}\right.$
解得,$\left\{\begin{array}{l}{c=90}\\{d=-90}\end{array}\right.$
即当1<t≤$\frac{4}{3}$时,y=90t-90;
当$\frac{4}{3}<t≤\frac{5}{3}$时,设y=et+f,
则$\left\{\begin{array}{l}{\frac{4}{3}e+f=90×\frac{1}{3}}\\{\frac{5}{3}e+f=0}\end{array}\right.$
解得,$\left\{\begin{array}{l}{e=-90}\\{f=150}\end{array}\right.$
即当$\frac{4}{3}<t≤\frac{5}{3}$时,设y=-90t+150;
由上可得,${y}_{汽车}=\left\{\begin{array}{l}{-90t+90}&{0≤t≤1}\\{90t-90}&{1<t≤\frac{4}{3}}\\{-90t+150}&{\frac{4}{3}<t≤\frac{5}{3}}\end{array}\right.$;
(3)由题意可得,
先遣分队的速度为:$\frac{60-30}{\frac{4}{3}-\frac{1}{3}}=\frac{30}{1}=30km/h$,
即先遣分队的速度是30km/h;
(4)由题意可得,
先遣分队比大部队早出发的时间为:$\frac{90×\frac{1}{3}-30×\frac{1}{3}}{30}=\frac{30-10}{30}=\frac{2}{3}$小时,
即先遣分队比大部队早出发$\frac{2}{3}$小时.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


科目:初中数学 来源: 题型:解答题
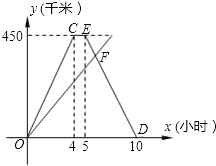 A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.
A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )
如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
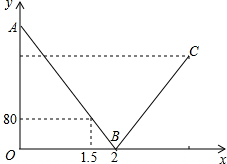 一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶80千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图象提供的信息,解答下列问题:
一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶80千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | a6÷a2=a3 | C. | (π-3)0=1 | D. | (2a)3=6a3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com