
【题目】如图,在平面直角坐标系中,A(0,1),B(2,0),C(4,3).
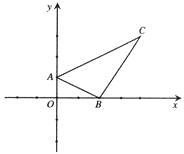
(1)求ΔABC的面积;
(2)设点P在坐标轴上,且ΔABP与ΔABC的面积相等,求点P的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
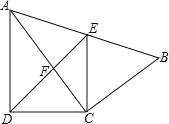
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=5,AB=8,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣5x>0.
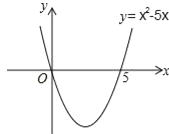
解:设x2﹣5x=0,解得:x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2﹣5x<0的解集为 .
(3)用类似的方法写出一元二次不等式的解集:x2﹣2x﹣3>0. .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,求∠MNA的度数.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.求BC的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句:
①一个数的绝对值一定是正数;
②﹣a一定是一个负数;
③没有绝对值为﹣3的数;
④若|a|=a,则a是一个正数;
⑤在原点左边离原点越远的数就越小;
正确的有( )个.
A.0
B.3
C.2
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
x | … | ﹣3 | - | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出2条函数的性质;
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所对应的方程x2﹣2|x|=0有
②方程x2﹣2|x|=2有 个实数根.
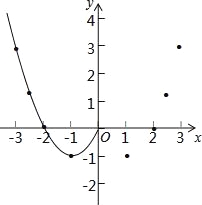
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com