
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE⊥AC于点E,BE与CD交于点F。

(1)求证:△ACD≌△FBD。
(2)若AB=5,AD=1,求BF的长。
【答案】(1)见解析;(2)![]()
【解析】
(1)由等腰直角三角形的性质推出BD=CD,再由等角的余角相等求得 ∠ACD=∠FBD ,于是根据角边角定理即可证明 △ACD和△FBD全等.
(2)由全等三角形对应边相等得出FD的长,于是在△BFD中,利用勾股定理即可求出BF的长.
(1)∵∠ABC=45°,CD⊥AB,
∴∠CDB=∠CDA=90°,
∴△CDB为等腰直角三角形
∴BD=CD
∵BE上AC
∴∠CEF=∠FDB=90°
又∵∠CFE=∠BFD
∴∠ACD=∠FBD
在△ACD和△FBD中
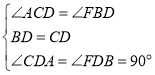
∴△ACD≌△FBD(ASA)
(2)由(1)知AD=FD=1,又AB=5,
∴BD=4
在Rt△BDF中,
BF= ![]()


科目:初中数学 来源: 题型:
【题目】如图,已知点A在反比例函数y=﹣![]() 的图象上,点D在反比例函数y=
的图象上,点D在反比例函数y=![]() (k≠0)的图象上,AD∥x轴,AB⊥x轴于B,DC⊥x轴于C,若OB=
(k≠0)的图象上,AD∥x轴,AB⊥x轴于B,DC⊥x轴于C,若OB=![]() OC,则k的值为_____.
OC,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了提高学生的消防意识,举行了消防知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已绘制成如图所示的两幅不完整的统计图,根据图中所经信息解答下列问题:
(1)这次知识竞赛共有多少名学生?
(2)“二等奖”对应的扇形圆心角度数,并将条形统计图补充完整;
(3)小华参加了此次的知识竞赛,请你帮他求出获得“一等奖或二等奖”的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)若![]() ,则
,则![]() 的度数是 ;
的度数是 ;
(2)若![]() ,
,![]() 的周长是
的周长是![]() .
.
①求![]() 的长度;
的长度;
②若点![]() 为直线
为直线![]() 上一点,请你直接写出
上一点,请你直接写出![]() 周长的最小值.
周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百子回归图是由 1,2,3,…,100 无重复排列而成的正方形数表,它是一部数化的澳门简史,如:中央四 位“19 99 12 20”标示澳门回归日期,最后一行中间两 位“23 50”标示澳门面积,…,同时它也是十阶幻方, 其每行 10 个数之和、每列 10 个数之和、每条对角线10 个数之和均相等,则这个和为______.
百 子 回 归

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B坐标为(-3,0),点A是y轴正半轴上一点,且AB=5,点P是x轴上位于点B右侧的一个动点,设点P的坐标为(m,0)

(1)点A的坐标为( )
(2)当△ABP是等腰三角形时,求P点的坐标;
(3)如图2,过点P作PE⊥AB交线段AB于点E,连接OE.若点A关于直线OE的对称点为A',当点A'恰好落在直线PE上时,BE=________(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=128°,则∠A的度数是( )
A.60°B.76°C.77°D.78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在
在![]() 的
的![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,若添加条件________,则四边形
,若添加条件________,则四边形![]() 是矩形;若添加条件________,则四边形
是矩形;若添加条件________,则四边形![]() 是菱形;若添加条件________,则四边形
是菱形;若添加条件________,则四边形![]() 是正方形.
是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B是数轴上两点,点A对应的数是-2,点B对应的数是2. △ABC是等边三角形,D是AB中点. 点M在AC边上,且AM=3CM.
(1)求CD长.
(2)点P是CD上的动点,确定点P使得PM+PA的值最小,并求出PM+PA的最小值.
(3)过点M的直线与数轴交于点Q,且QM![]() .点Q对应的数是t,结合图形直接写出t的取值范围.
.点Q对应的数是t,结合图形直接写出t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com