
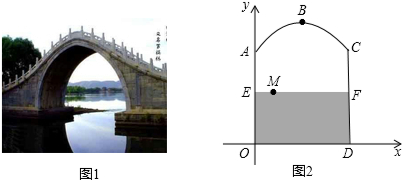
分析 (1)根据题意得出B点坐标,进而利用顶点式求出函数解析式即可;
(2)利用勾股定理得出AE的长进而得出答案;
(3)利用已知函数解析式结合题意得出h=7时的时间,进而得出答案.
解答 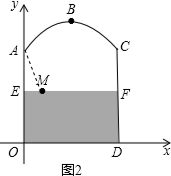 解:(1)由题意可得:AO=CD=8m,B点纵坐标为:1.5×8=12,则B点坐标为:(5,12),
解:(1)由题意可得:AO=CD=8m,B点纵坐标为:1.5×8=12,则B点坐标为:(5,12),
设抛物线解析式为:y=a(x-5)2+12,将A(0,8)代入解析式得:
8=a(0-5)2+12,
解得:a=-$\frac{4}{25}$.
故抛物线解析式为:y=-$\frac{4}{25}$(x-5)2+12;
(2)连接AM,
由题意可得:AM=2.5m,EM=1.5m,
在Rt△AEM中,AE=$\sqrt{A{M}^{2}+E{M}^{2}}$=2(m),
则EO=8-2=6(m),故此时河水的高度为6米;
(3)当水面到顶点B的距离为5米时,此时h=7,则7=-$\frac{1}{128}$(t-17)2+9,
解得:t1=1,t2=33.
则在1~33小时这段时间内,即需要33-1=32(小时)禁止船只通行.
点评 此题主要考查了二次函数的应用以及勾股定理等知识,根据题意得出B点坐标是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,把一块边长为6的正方形纸片ABCD沿着PQ翻折,使顶点A恰好与CD边上的点E重合,若DE=2,则折痕PQ=2$\sqrt{10}$.
如图,把一块边长为6的正方形纸片ABCD沿着PQ翻折,使顶点A恰好与CD边上的点E重合,若DE=2,则折痕PQ=2$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com