
| x1+x2 |
| 2 |
| 6 |
| 6 |
| 6 |
| 6 |


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源:2013年江苏省东台市实验中学中考数学模拟试卷(带解析) 题型:解答题
若抛物线的顶点坐标是(1,16),并且抛物线与 轴两交点间的距离为8,(1)试求该抛物线的关系式;
轴两交点间的距离为8,(1)试求该抛物线的关系式;
(2)求出这条抛物线上纵坐标为12的点的坐标。
查看答案和解析>>
科目:初中数学 来源:《第27章 二次函数》2010年单元测试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:《第26章 二次函数》2009年旧口高中单元测试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2013年江苏省东台市中考数学模拟试卷(解析版) 题型:解答题
若抛物线的顶点坐标是(1,16),并且抛物线与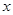 轴两交点间的距离为8,(1)试求该抛物线的关系式;
轴两交点间的距离为8,(1)试求该抛物线的关系式;
(2)求出这条抛物线上纵坐标为12的点的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com