
����Ŀ��������ABCD�ı߳�Ϊ4����������������ƽ��ֱ������ϵ�У�ʹAB������X����������ϣ���A��������ǣ�1��0����
��1��ֱ��![]() ������C������x�ύ���E�����ı���AECD�������
������C������x�ύ���E�����ı���AECD�������
��2����ֱ��l������E���ҽ�������ABCD�ֳ������ȵ������֣���ֱ��l�Ľ���ʽ��
��3����ֱ��l1������F����![]() ��0��������ֱ��y=3xƽ�У�����2����ֱ��l����y������ƽ��
��0��������ֱ��y=3xƽ�У�����2����ֱ��l����y������ƽ��![]() ����λ����x�ڵ�M����ֱ��l1�ڵ�N������NMF�������
����λ����x�ڵ�M����ֱ��l1�ڵ�N������NMF�������

���𰸡���1���ı���AECD�����Ϊ10����2��ֱ��l�Ľ���ʽΪy=2x-4����3��![]()
�������������������1��������֪�߳��Ѿ����ߣ������ı��ε������
��2��ֱ��l������E�ҽ�������ABCD�ֳ������ȵ������֣�����DC���ڵ�F�����������ε����ʣ������F�����꣬��ֱ��l�Ľ���ʽ��y=kx+b����E��F��������뼴���������ʽ��
��3������ֱ��l1������F����![]() ��0������ֱ��y=3xƽ�У�֪k=3����F��������뼴�����b��ֵ���ɵó�ֱ��11��ͬ���������ʽy=2x-3����һ�����M��N�����꣬���������ε������ʽ���������MNF�������
��0������ֱ��y=3xƽ�У�֪k=3����F��������뼴�����b��ֵ���ɵó�ֱ��11��ͬ���������ʽy=2x-3����һ�����M��N�����꣬���������ε������ʽ���������MNF�������
�����������1����y=![]() x
x![]() ����y=4����
����y=4����![]() x
x![]() =4����ã�x=5����B�������ǣ�5��0����
=4����ã�x=5����B�������ǣ�5��0����
��y=0����![]() x
x![]() =0����ã�x=2����E�������ǣ�2��0����
=0����ã�x=2����E�������ǣ�2��0����
��OB=5��OE=2��BE=OB��OA=5��2=3����AE=AB��BE=4��3=1��
�ı���AECD�����=![]() ��AE+CD��AD=
��AE+CD��AD=![]() ��4+1����4=10��
��4+1����4=10��
��2��������E�ҽ�������ABCD�ֳ������ȵ������֣���ֱ����CD�Ľ���F������CF=AE=1����F�������ǣ�4��4����
��ֱ�ߵĽ���ʽ��y=kx+b����![]() ����ã�
����ã� ![]() ��
��
��ֱ��l�Ľ���ʽ�ǣ�y=2x��4��
��3����ֱ��l1������F����![]() ��0������ֱ��y=3xƽ�У�
��0������ֱ��y=3xƽ�У�
��ֱ��11�Ľ���ʽ��y1=kx+b����k=3��
����ã�0=3������![]() ��+b����ã�b=
��+b����ã�b=![]() ��
��
��y1=3x+![]() ��
��
��֪����2����ֱ��l����y������ƽ��![]() ����λ�������õ�ֱ�ߵĽ���ʽ��y=2x��4+
����λ�������õ�ֱ�ߵĽ���ʽ��y=2x��4+![]() ��
��
����y=2x��3![]() ����y=0ʱ��x=
����y=0ʱ��x=![]() ����M��
����M��![]() ��0����
��0����
�ⷽ����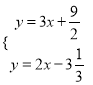 �ã�
�ã� 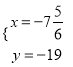 ������N����7
������N����7![]() ����19����
����19����
S��NMF=![]() ��[
��[![]() ������
������![]() ��]��|��19|=
��]��|��19|=![]() ��
��
����NMF�������![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB����COD�ǵ���ֱ�������Σ���D��AB�ϣ�
��1����֤����AOC�ա�BOD��
��2����AD=3��BD=1����CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ŵ�һ����180Ԫ������8��ͯ��װ����һ���۸����.�����ÿ��ͯ��װ80Ԫ�ļ۸�Ϊ���������ļ�������������ļ�����������¼���£���λ��Ԫ����
![]()
��ͨ������˵����
��1��С��������8��ͯ��װ����ӯ�����ǿ���ӯ����������˶���Ǯ��
��2��ÿ��ͯ��װ��ƽ���ۼ��Ƕ���Ԫ��
��3��С�ŵڶ����õ�һ�εĽ����ٴι���900Ԫ�Ķ�ͯ��װ�������Ԥ�Ƶڶ���ÿ��װ��ƽ���ۼ�75Ԫ��������Ԥ�Ƶڶ����ۼۿɻ�������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��x�ᡢy��ֱ��ڵ�A��B����C���߶�AB��һ�㣬�ı���OADC�����Σ���OD�ij�.
��x�ᡢy��ֱ��ڵ�A��B����C���߶�AB��һ�㣬�ı���OADC�����Σ���OD�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯ѧ��������ѧУ6ǧ�ĿƼ���ȥ�ιۣ�С������û�ܳ���ѧУ�İ�������������ѧУ�ſڸij˳��ȥ�Ƽ��ݣ�����շѱ����������ͣ����±���
��� | �����շѣ�Ԫ�� | �����շѣ�Ԫ�� |
3ǧ�����£�����3ǧ�ף� | 7.00 | 6.00 |
3ǧ�����ϣ�ÿ����1ǧ�� | 1.60 | 1.40 |
��1��������ʻ�����Ϊxǧ�ף�![]() ��xȡ�����������ֱ�д���������͵����շѣ��ú�x�Ĵ���ʽ��ʾ����
��xȡ�����������ֱ�д���������͵����շѣ��ú�x�Ĵ���ʽ��ʾ����
��2��С�����Ͻ���11Ԫ�����˳�����Ƽ��ݳ��ѹ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O��ֱ��AB�ϵ�һ�㣬![]() ��ֱ�ǣ�OEƽ��
��ֱ�ǣ�OEƽ��![]() ��
��
��1����ͼ1����![]() ����
����![]() �Ķ�����
�Ķ�����
��2����ͼ1�У�![]() ��ֱ��д��
��ֱ��д��![]() �Ķ������ú�a�Ĵ���ʽ��ʾ����
�Ķ������ú�a�Ĵ���ʽ��ʾ����
��3����ͼ1�е�![]() �ƶ���O˳ʱ����ת��ͼ2��λ�ã�̽��
�ƶ���O˳ʱ����ת��ͼ2��λ�ã�̽��![]() ��
��![]() �Ķ���֮��Ĺ�ϵ��д����Ľ��ۣ���˵�����ɣ�
�Ķ���֮��Ĺ�ϵ��д����Ľ��ۣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=5��AD=3����P��AB����һ�㣨����A��B�غϣ�������CP������P��PQ��CP��AD�ڵ�Q������CQ��ȡCQ���е�M������MD��MP����MD��MP����AQ�ij�________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O��ԭ�㡣
��1����ͼ�٣���C������Ϊ��![]() ��
��![]() ������ʵ��
������ʵ��![]() ��
��![]() ����
����![]() ����C������꼰�߶�0C�ij��ȣ�
����C������꼰�߶�0C�ij��ȣ�
��2����ͼ�ڣ���F��BC�ϣ�AB��x���ڵ�E��EF��OC���ӳ��߽��ڵ�G��EG=OG�����EOF�Ķ�����
��3����ͼ�ۣ�����1����������OABC�Ƶ�O˳ʱ����ת��ʹOA����y���ϣ�EΪAB������һ�㣬OE�Ĵ�ֱƽ���߽�x���ڵ�G����OE�ڵ�P,����EG��BC�ڵ�F�����BEF���ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��![]() .
.
(1)����A��
(2)��a��3ʱ���Ǵ�ʱA��ֵΪf(3)����a��4ʱ���Ǵ�ʱA��ֵΪf(4)���������x�IJ���ʽ��![]() ��
��![]() ��f(3)��f(4)������f(11)���������Ľ⼯�������ϱ�ʾ������
��f(3)��f(4)������f(11)���������Ľ⼯�������ϱ�ʾ������
![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com