
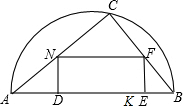
 如图,在直径为AB的半圆内,画出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,其它两边分别为6和8,现要建造一个内接于△ABC的矩形建筑物DEFN,其中DE在AB上,设计方案是使AC=8,BC=6.
如图,在直径为AB的半圆内,画出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,其它两边分别为6和8,现要建造一个内接于△ABC的矩形建筑物DEFN,其中DE在AB上,设计方案是使AC=8,BC=6. =
= =10,
=10,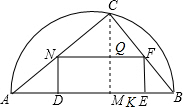
 AC×BC=
AC×BC= AB×h,
AB×h, =
= =4.8
=4.8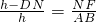

 =-
=- (x-2.4)2+12,
(x-2.4)2+12, =4.8,
=4.8, CM=2.4,
CM=2.4, BC=3,
BC=3,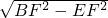 =
= =1.8
=1.8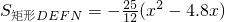 ,利用二次函数的性质求关系式的最大值.
,利用二次函数的性质求关系式的最大值.

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
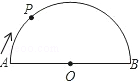
 (2013•贵阳)如图,在直径为AB的半圆O上有一动点P从A点出发,按顺时针方向绕半圆匀速运动到B点,然后再以相同的速度沿着直径回到A点停止,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )
(2013•贵阳)如图,在直径为AB的半圆O上有一动点P从A点出发,按顺时针方向绕半圆匀速运动到B点,然后再以相同的速度沿着直径回到A点停止,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直径为AB的一块半圆形土地上,画出一块三角形区域,使三角形的一边为AB,顶点C在半圆上,其它两边长分别为6cm和8cm,现要建造一个内接于△ABC的矩形水池DEFN,其中DE在AB上,如图所示的设计方案是使AC=8cm,BC=6cm。
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85m处有一棵大树,则这棵大树是否位于最大矩形的边上?如果在,为了保护大树,请你设计出另外的方案,使内接于满足条件的三角形中建最大矩形水池能避开大树。

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直径为AB的半圆O上有一动点P从A点出发,按顺时针方向绕半圆匀速运动到B点,然后再以相同的速度沿着直径回到A点停止,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是
A.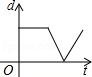 B.
B.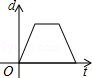 C.
C.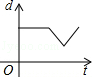 D.
D.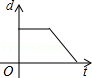
查看答案和解析>>
科目:初中数学 来源:2012届江苏省沭阳银河学校九年级下学期质量检测数学卷 题型:解答题
如图,在直径为AB的一块半圆形土地上,画出一块三角形区域,使三角形的一边为AB,顶点C在半圆上,其它两边长分别为6cm和8cm,现要建造一个内接于△ABC的矩形水池DEFN,其中DE在AB上,如图所示的设计方案是使AC=8cm,BC=6cm。
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85m处有一棵大树,则这棵大树是否位于最大矩形的边上?如果在,为了保护大树,请你设计出另外的方案,使内接于满足条件的三角形中建最大矩形水池能避开大树。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com