
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )

A. ②③ B. ③④ C. ①②④ D. ②③④
【答案】D
【解析】∵矩形ABCD,
∴AD∥BC,![]() ,AO=OC,OD=OB,AC=BD,
,AO=OC,OD=OB,AC=BD,
∴AO=OB=OD,
∵AB=1,AD=![]() ,由勾股定理得:AC=2,
,由勾股定理得:AC=2,
∴∠ABD=60°,
∴△ABO是等边三角形,
∴AB=OA=OB, ∠BAO=∠AOB=60°,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵∠DAF=∠AFB,
∴∠BAF=∠BFA,![]() ,∴②正确;
,∴②正确;
∵CE⊥BD,![]() ,
,
∴∠ECO=30°,![]() ,
,![]() ,
,
∴AC=CH, ∴③正确;
∵CF和AH不垂直, ∴AF≠FH, ∴①错误;
∵∠CEO=90°, ∠ECA=30°,![]() ,
,
BE=3DE, ∴④正确.
正确的有②③④,故选D.
点睛;本题主要考查对等腰三角形的性质,勾股定理,三角形的外角性质,矩形的性质,平行线的性质,等边三角形的性质和判定等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.


科目:初中数学 来源: 题型:
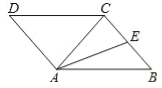
【题目】如图,在ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
北京时间 | 7:30 | 11:15 | 2:50 |
首尔时间 | 8:30 | 12:15 | 3:50 |
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )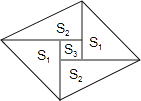
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.
![]()
(1)求线段BC的长;
(2)求线段MN的长;
(3)若C在线段AB延长线上,且满足AC﹣BC=b cm,M,N分别是线段AC,BC的中点,你能猜想MN的长度吗?请写出你的结论(不需要说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中共中央国务院关于深化教育改革全面推进素质教育的决定》中明确指出:“健康体魄是青少年为祖国和人民服务的基本前提,是中华民族旺盛生命力的体现.” 王老师所在的学校为加强学生的体育锻炼,需购买若干个足球和篮球,他曾三次在某商场购买过足球和篮球,其中有一次购买时,遇到商场打折销售,其余两次均按标价购买,三次购买足球和篮球的数量和费用如下表:

(1)王老师是第_____次购买足球和篮球时,遇到商场打折销售的;
(2)求足球和篮球的标价;
(3)如果现在商场均以标价的6折对足球和篮球进行促销,万老师决定从商场一次性购买足球和篮球60个,且总费用不能超过2500元,那么最多可以购买 _____ 个篮球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC= ![]() ,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG.
,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG. 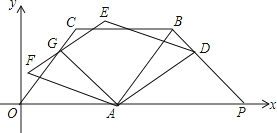
(1)求点B的坐标.
(2)当OG=4时,求AG的长.
(3)求证:GA平分∠OGE.
(4)连结BD并延长交x轴于点P,当点P的坐标为(12,0)时,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
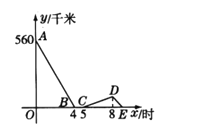
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后停留一段时间,然后分别按原速一同驶往甲地后停车。设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲、乙两地之间的距离为________千米;
(2)求快车和慢车的速度。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com