
【题目】如图,在△ABC中,AC=BC,CD是边AB上的高线,且有2CD=3AB=6,CE=EF=DF,则下列判断中不正确的是( )

A. ∠AFB=90 B. BE=![]() C. △EFB∽△BFC D. ∠ACB+∠AEB=45°
C. △EFB∽△BFC D. ∠ACB+∠AEB=45°
【答案】D
【解析】
由于AC=BC,CD是AB边上的高线,可知BD=1,且CD是AB的垂直平分线,利用2CD=3AB,易求CD=3,再利用垂直平分线的定理易求∠ACB=2∠BCE,∠AEB=2∠BEF,求出CE=EF=DF=1,易证△DBF是等腰直角三角形,再利用勾股定理可求BF=![]() ,可求
,可求![]() ,而夹角相等易证△EFB∽△BFC,那么有∠FBE=∠BCF,∠FEB=∠FBC,结合三角形外角的性质易证∠ACB+∠AEB=90°.
,而夹角相等易证△EFB∽△BFC,那么有∠FBE=∠BCF,∠FEB=∠FBC,结合三角形外角的性质易证∠ACB+∠AEB=90°.
∵AC=BC,CD是AB边上的高线,3AB=6,
∴BD=AD=![]() AB=1,CD是AB的垂直平分线,
AB=1,CD是AB的垂直平分线,
又∵2CD=3AB=6,AE=BE,AF=BF,
∴CD=3,∠ACB=2∠BCE,∠AEB=2∠BEF,
∵CE=EF=DF,
∴CE=EF=DF=1,
∴DF=DB=1,
又∵∠CDB=90°,
∴BE=![]() ,选项B正确,
,选项B正确,
△DBF、△DFA是等腰直角三角形,
∴∠DFB=∠DFA=45°,BF=![]() ,
,
∴∠AFB=90°,选项A正确,
![]() ,
,![]() ,
,
∴![]() ,
,
又∵∠EFB=∠BFC,
∴△EFB∽△BFC,选项C正确,
∴∠FBE=∠BCF,∠FEB=∠FBC,
又∵∠DFB=∠FBE+∠FEB=∠FCB+∠FBC,
∴45°=∠FBE+∠FEB,
∴90°=2∠FBE+2∠FEB=2∠BCF+2∠FBC,
∴∠ACB+∠AEB=90°,选项D错误.
故选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知线段a=0.3m,b=60cm,c=12dm.
(1)求线段a与线段b的比.
(2)如果线段a、b、c、d成比例,求线段d的长.
(3)b是a和c的比例中项吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)株洲五桥主桥主孔为拱梁钢构组合体系(如图1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,发现可以将余下的8根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个相似三角形,他们的周长分别是36和12.周长较大的三角形的最大边为15,周长较小的三角形的最小边为3,则周长较大的三角形的面积是()
A. 52 B. 54 C. 56 D. 58.
查看答案和解析>>
科目:初中数学 来源: 题型:
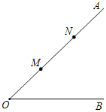
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=3,ON=7,点P是直线OB上的点,要使点P,M,N构成等腰三角形的点P有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小泽和小超分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小泽掷得的点数为x,小超掷得的点数为![]() ,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com