
����Ŀ��С��������Ƶ�ʹ��Ƹ��ʡ���ʵ��ʱ������ͳ�ƽ������������ͼ��ʾ������ͳ��ͼ���������һ�����ʵ�����п��ܵ��ǣ� �� 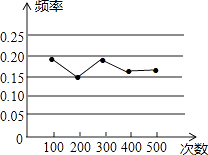
A.ͬʱ������öӲ�ң���غ���öӲ�����涼����
B.һ��ȥ����С�����˿��ƣ�ϴ�Ⱥ����γ�һ���ƵĻ�ɫ�Ǻ���
C.��һ���ʵؾ��ȵ����������ӣ����ϵ��������3
D.һ�������Ĵ�������4������1���������dz�����ɫ�ⶼ��ͬ�����г鵽����
���𰸡�C
���������⣺A��ͬʱ������öӲ�ң���غ���öӲ�����涼���ϵĸ���Ϊ ![]() ����Aѡ����� B��һ��ȥ����С�����˿��ƣ�ϴ�Ⱥ����γ�һ���ƵĻ�ɫ�Ǻ��ҵĸ�����
����Aѡ����� B��һ��ȥ����С�����˿��ƣ�ϴ�Ⱥ����γ�һ���ƵĻ�ɫ�Ǻ��ҵĸ����� ![]() ����Bѡ�����
����Bѡ�����
C����һ���ʵؾ��ȵ����������ӣ����ϵ��������3�ĸ����� ![]() ��0.17����Cѡ����ȷ��
��0.17����Cѡ����ȷ��
D��һ�������Ĵ�������4������1���������dz�����ɫ�ⶼ��ͬ�����г鵽����ĸ���Ϊ ![]() ��Dѡ�����
��Dѡ�����
��ѡ��C��
�����㾫��������Ƶ������ͼ����Ƶ�ʹ��Ƹ��ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪������ر�ʾ���ռ������õ��ĸ����Ƶ�����仯����ͬ�������£����������ظ����飬����һ������¼�������Ƶ�����ȶ���ij�����������Թ�������¼������ĸ��ʣ�


 ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x-1����x99+x98+x97+��+x+1����ֵ��
�������������⣬���ǿ�����˼��һ�£��Ӽ��������֣�
�ֱ�������и�ʽ��ֵ��
��1����x��1����x+1��=x2��1��
��2����x��1����x2+x+1��=x3��1��
��3����x��1����x3+x2+x+1��=x4��1��
��
�ɴ����ǿ��Եõ�����x��1����x99+x98+x97+��+x+1��= _________ ��
������������Ľ��ۣ������������ļ��㣺
��1��299+298+297+��+2+1��
��2������2��50+����2��49+����2��48+��+����2��+1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��B��C��E ������ͬһ��ֱ���ϣ�AB��DC��BC=DC����ACD=��E.
��֤����1����ACB=��D��
��2��AB=EC.
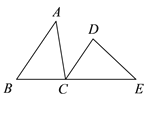
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABC�У���֪�߶�ADƽ����BAC��BC��D����B=62�㣬��C=58�㣮
��1���ó߹������߶�AD��������ADB�Ķ�����
��2����DE��AC�ڵ�E����ͼ�β�������������ADE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC��90�㣬AB��BC��D��AC��һ�㣬AE��BD����BD���ӳ�����E��CF��BD��F.
(1)��֤��CF��BE��
(2)��BD��2AE����֤����EAD����ABE.
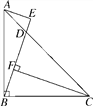
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ���״�̽������ʾ��ͼ,̽������λ����O��(Բ��λ��),�������ͬ��Բ�İ뾶����Ϊ1km,2km,3km,4km,5km,6km,�����Ե�OΪ���յ�,�÷�λ�Ǻ;���ֱ��ʾ�״�̽����̽���Ŀ��A,B,C,D,E,F��λ��.
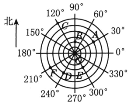
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��9��10�գ�֣�������ʽ��Ӫ�������ݵ�֣��ȫ��Լ360km��������ͨ������ʱ����ؿ��г����õ�ʱ�������2.1Сʱ���������г���ƽ���ٶ����ؿ��г�ƽ���ٶȵ�2.4�������ؿ��г���ƽ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AD=4����E�ǶԽ���AC��һ�㣬����DE������E��EF��ED����AB�ڵ�F������DF����AC�ڵ�G������EFG��EF���ۣ��õ���EFM������DM����EF�ڵ�N������F��AB���е㣬���EMN���ܳ��� �� 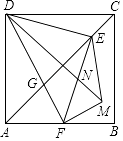
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ����֪��C���߶�AB�ϣ���AC=5cm,BC=3cm,��M,N�ֱ���AC��BC���е㣬���߶�MN�ij���.
��2������C���߶�AB������һ�㣬��AC=a,BC=b, ��M��N�ֱ��ǣ�AC��BC���е㣬��ֱ��д���߶�MN�ij��ȣ��ú�a��b�Ĵ���ʽ��ʾ��
![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com