
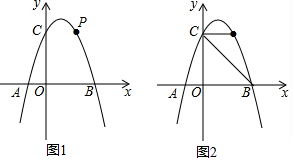
分析 (1)利用三角形的面积求出a即可得出抛物线解析式;
(2)先判断出∠OBC=45°,而点P在第一象限,所以得出CP∥OB即:点P和点C的纵坐标一样,即可确定出点P坐标;
(3)根据点P在第一象限,点Q在第二象限,且横坐标相差1,进而设出点P(3-m,-m2+4m)(0<m<1);得出点Q(4-m,-m2+6m-5),得出CP2,AQ2,最后建立方程求解即可.
解答 解:(1)∵抛物线y=ax2-2ax-3a=a(x+1)(x-3),
∴A(-1,0),B(3,0),C(0,-3a),
∴AB=4,OC=|-3a|=|3a|,
∵S△ABC=6,
∴$\frac{1}{2}$AB•OC=6,
∴$\frac{1}{2}$×4×|3a|=6,
∴a=-1或a=1(舍),
∴抛物线的解析式为y=-x2+2x+3;
(2)由(1)知,B(3,0),C(0,-3a),
∴C(0,3),
∴OB=3,OC=3,
∴△OBC是等腰直角三角形,
∴∠BCO=∠OBC=45°,
∵点P为第一象限内抛物线上的一点,且∠PCB=45°,
∴PC∥OB,
∴P点的纵坐标为3,
由(1)知,抛物线的解析式为y=-x2+2x+3,
令y=3,∴-x2+2x+3=3,
∴x=0(舍)或x=2,
∴P(2,3);
(3)如图2,过点P作PD⊥x轴交CQ于D,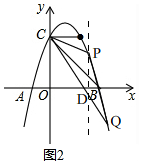 设P(3-m,-m2+4m)(0<m<1);
设P(3-m,-m2+4m)(0<m<1);
∵C(0,3),
∴PC2=(3-m)2+(-m2+4m-3)2=(m-3)2[(m-1)2+1],
∵点Q的横坐标比点P的横坐标大1,
∴Q(4-m,-m2+6m-5),
∵A(-1,0).
∴AQ2=(4-m+1)2+(-m2+6m-5)2=(m-5)2[(m-1)2+1]
∵PC=$\frac{5}{9}$AQ,
∴81PC2=25AQ2,
∴81(m-3)2[(m-1)2+1]=25(m-5)2[(m-1)2+1],
∵0<m<1,
∴[(m-1)2+1]≠0,
∴81(m-3)2=25(m-5)2,
∴9(m-3)=±5(m-5),
∴m=$\frac{1}{2}$或m=$\frac{26}{7}$(舍),
∴P($\frac{5}{2}$,$\frac{7}{4}$),Q($\frac{7}{2}$,-$\frac{9}{4}$),
∵C(0,3),
∴直线CQ的解析式为y=-$\frac{3}{2}$x+3,
∵P($\frac{5}{2}$,$\frac{7}{4}$),
∴D($\frac{5}{2}$,-$\frac{3}{4}$),
∴PD=$\frac{7}{4}$+$\frac{3}{4}$=$\frac{5}{2}$,
∴S△PCQ=S△PCD+S△PQD=$\frac{1}{2}$PD×xP+$\frac{1}{2}$PD×(xQ-xP)=$\frac{1}{2}$PD×xQ=$\frac{1}{2}$×$\frac{5}{2}$×$\frac{7}{2}$=$\frac{35}{8}$.
点评 此题是二次函数综合题,主要考查了待定系数法,三角形的面积公式,平行线的性质和判定,解本题的关键是判断出PC∥OB,难点是设出点P的坐标,是一道比较好的中考常考题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
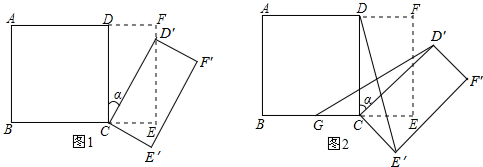
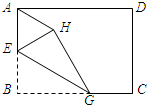 如图,已知长方形纸片ABCD,点E是AB的中点,点G是BC上一点,∠BEG=60°.沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )
如图,已知长方形纸片ABCD,点E是AB的中点,点G是BC上一点,∠BEG=60°.沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
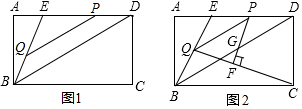
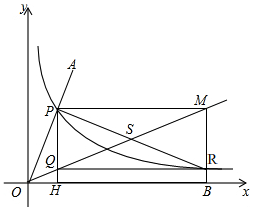 如图,在平面直角坐标系中,射线OA交反比例函数y=$\frac{1}{x}$(x>0)图象于点P,点R为反比例函数y=$\frac{1}{x}$(x>0)图象上的另一点,且PR=2OP,分别过点P、R作x轴、y轴的平行线,两线相交于点M(a,b),直线MR交x轴于点B,过点P作y轴的平行线分别交直线OM和x轴于点Q、H,连接RQ.
如图,在平面直角坐标系中,射线OA交反比例函数y=$\frac{1}{x}$(x>0)图象于点P,点R为反比例函数y=$\frac{1}{x}$(x>0)图象上的另一点,且PR=2OP,分别过点P、R作x轴、y轴的平行线,两线相交于点M(a,b),直线MR交x轴于点B,过点P作y轴的平行线分别交直线OM和x轴于点Q、H,连接RQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
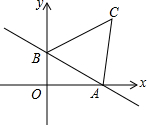 一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC
一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com