
分析 令x=0,则y=2-a,令y=0则x=$\frac{a-2}{a}$,得到A($\frac{a-2}{a}$,0),B(0,2-a),由△ABO外接圆的圆心为点C得到点C是AB的中点,求得C($\frac{a-2}{2a}$,$\frac{2-a}{2}$),当点O到直线l距离最大时,△ABC是等腰直角三角形,根据等腰直角三角形的性质得到AO=BO,于是得到结论.
解答 解:∵直线l:y=ax-a+2与x轴交于点A,与y轴交于点B,
令x=0,则y=2-a,令y=0则x=$\frac{a-2}{a}$,
∴A($\frac{a-2}{a}$,0),B(0,2-a),
∵O点为坐标原点,
∴∠AOB=90°,
∵△ABO外接圆的圆心为点C,
∴点C是AB的中点,
∴C($\frac{a-2}{2a}$,$\frac{2-a}{2}$),
当点O到直线l距离最大时,△ABC是等腰直角三角形,
∴AO=BO,
∴$\frac{a-2}{a}$=2-a,
解得:a=2或a=-1,
当a=-1时,C($\frac{3}{2}$,$\frac{3}{2}$),
∴k=$\frac{9}{4}$,
当a=2时,C(0,0)(不合题意,舍去)
∴k=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查了三角形的外接圆与外心,等腰直角三角形的性质,反比例函数图象上点的坐标特征,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
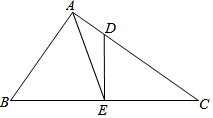 如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.
如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).| 分组/元 | 频 数 | 频 率 |
| 1000<x<1200 | 3 | 0.060 |
| 1200<x<1400 | 12 | 0.240 |
| 1400<x<1600 | 18 | 0.360 |
| 1600<x<1800 | a | 0.200 |
| 1800<x<2000 | 5 | b |
| 2000<x<2200 | 2 | 0.040 |
| 合计 | 50 | 1.000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 方式 | 频数 | 百分比 |
| 网络 | 23 | 46% |
| 电视 | ||
| 报纸 | 8% | |
| 其他 | 15 | |
| 合计 | 100% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com