
【题目】(阅读)如图1,在等腰△ABC中,AB=AC,AC边上的高为h,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为h1,h2.连接AM.
∵![]() ∴
∴![]()
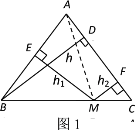
(思考)在上述问题中,h1,h2与h的数量关系为: .
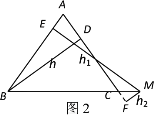
(探究)如图2,当点M在BC延长线上时,h1、h2、h之间有怎样的数量关系式?并说明理由.
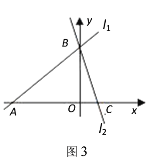
(应用)如图3,在平面直角坐标系中有两条直线l1:![]() ,l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用上述结论求出点M的坐标.
,l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用上述结论求出点M的坐标.
【答案】【思考】h1+h2=h;【探究】h1-h2=h.理由见解析;【应用】所求点M的坐标为(![]() ,2)或(-
,2)或(-![]() ,4).
,4).
【解析】
思考:根据等腰三角形的性质,把代数式![]() 化简可得
化简可得![]() .
.
探究:当点M在BC延长线上时,连接![]() ,可得
,可得![]() ,化简可得
,化简可得![]() .
.
应用:先证明![]() ,△ABC为等腰三角形,即可运用上面得到的性质,再分点M在BC边上和在CB延长线上两种情况讨论,第一种有1+My=OB,第二种为My-1=OB,解得
,△ABC为等腰三角形,即可运用上面得到的性质,再分点M在BC边上和在CB延长线上两种情况讨论,第一种有1+My=OB,第二种为My-1=OB,解得![]() 的纵坐标,再分别代入
的纵坐标,再分别代入![]() 的解析式即可求解.
的解析式即可求解.
思考
![]()
![]()
即![]()
![]()
![]()
![]() h1+h2=h.
h1+h2=h.
探究
h1-h2=h.
理由.连接![]() ,
,
∵![]()
∴![]()
∴h1-h2=h.
应用
在![]() 中,令x=0得y=3;
中,令x=0得y=3;
令y=0得x=-4,则:
A(-4,0),B(0,3)
同理求得C(1,0),
![]() ,
,
又因为AC=5,
所以AB=AC,即△ABC为等腰三角形.
①当点M在BC边上时,
由h1+h2=h得:
1+My=OB,My=3-1=2,
把它代入y=-3x+3中求得:
![]() ,
,
∴![]() ;
;
②当点M在CB延长线上时,
由h1-h2=h得:
My-1=OB,My=3+1=4,
把它代入y=-3x+3中求得:
![]() ,
,
∴![]() ,
,
综上,所求点M的坐标为![]() 或
或![]() .
.


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】已知实数a,c满足![]() ,2a+c﹣ac+2>0,二次函数y=ax2+bx+9a经过点B(4,n)、A(2,n),且当1≤x≤2时,y=ax2+bx+9a的最大值与最小值之差是9,求a的值.
,2a+c﹣ac+2>0,二次函数y=ax2+bx+9a经过点B(4,n)、A(2,n),且当1≤x≤2时,y=ax2+bx+9a的最大值与最小值之差是9,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月销售216辆.
(1)求该品牌电动车销售量的月平均增长率;
(2)若该品牌电动自行车的进价为2300元,售价2800元,则该经销商1月至3月共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
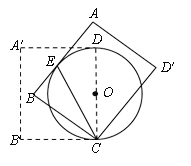
【题目】如图,在矩形A′B′CD中,A′B′=10, B′C=8,以CD为直径作⊙O.将矩形A′B′CD绕点C旋转,使所得矩形ABCD′的边AB与⊙O相切,切点为E.
(1)证明:CE平分∠BCD;
(2)求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A(﹣1,m),B(n,﹣1)两点.
的图象相交于A(﹣1,m),B(n,﹣1)两点.
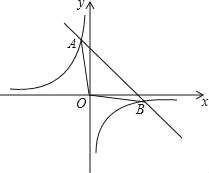
(1)求出这个一次函数的表达式.
(2)求△OAB的面积.
(3)直接写出使一次函数值大于反比例函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
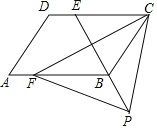
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图反映了我国出租车(巡游出租车和网约出租车)客运量结构变化.
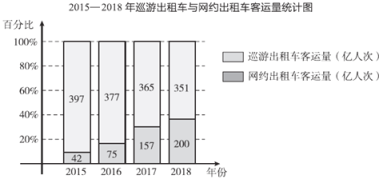
(以上数据摘自《中国共享经济发展年度报告(2019)》)
根据统计图提供的信息,下列推断合理的是( )
A.2018年与2017年相比,我国网约出租车客运量增加了20%以上
B.2018年,我国巡游出租车客运量占出租车客运总量的比例不足60%
C.2015年至2018年,我国出租车客运的总量一直未发生变化
D.2015年至2018年,我国巡游出租车客运量占出租车客运总量的比例逐年增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com