
分析 先确定抛物线y=-x2的顶点坐标为(0,0),再利用点平移的规律得到点(0,0)平移后所得对应点的坐标为(1,0),然后根据顶点式可得平移后的抛物线的解析式.
解答 解:抛物线y=-x2的顶点坐标为(0,0),把点(0,0)向右平移1个单位所得对应点的坐标为(1,0),所以平移后的抛物线的解析式是y=-(x-1)2.
故答案为y=-(x-1)2.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式


科目:初中数学 来源: 题型:解答题
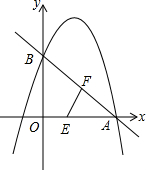 如图,抛物线y=-x2+bx+c(a≠0)与x轴、y轴分别交于点A(3,0)、B(0,3)两点.
如图,抛物线y=-x2+bx+c(a≠0)与x轴、y轴分别交于点A(3,0)、B(0,3)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{9}{4}$ | C. | 3 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
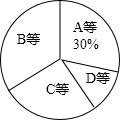 某校为了解七年级男生1000米跑步的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成频数分布表和扇形统计图.
某校为了解七年级男生1000米跑步的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成频数分布表和扇形统计图.| 等级 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | m | |
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | n | |
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com