
���� ��1����a-b+c=0���ɵó�b=a+c����ϸ������Ͽɲ²ⷽ�̵���������һ��Ϊ-1����һ��Ϊ-$\frac{c}{a}$�����������ʽ��ϸ��������е�֤�����̼���֤���²������
��2��������ϵ����Ӽ��ɵ�֪��ac-bc+bc-ab+ab-ac=0��������������ϵ��������ɴ˵ó����̵������ֱ�Ϊ1��$\frac{ab-ac}{ac-bc}$���������֪$\frac{ab-ac}{ac-bc}$=1���������κɵó����ۣ�
��� �⣺��1����һ��Ϊ-1����һ��Ϊ-$\frac{c}{a}$��
֤�����跽�̵�����Ϊx1��x2����a-b+c=0��
֪b=a+c��
��x=$\frac{-b��\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-��a+c����\sqrt{[-��a+c��]^{2}-4ac}}{2a}$=$\frac{-��a+c������a-c��}{2a}$��
��x1=-1��x2=-$\frac{c}{a}$��
��2��֤������ac-bc+bc-ab+ab-ac=0��
��̣�ac-bc��x2+��bc-ab��x+��ab-ac��=0��abc��0���������ֱ�Ϊ1��$\frac{ab-ac}{ac-bc}$��
�߷��̣�ac-bc��x2+��bc-ab��x+��ab-ac��=0��abc��0����������ȵ�ʵ������
��$\frac{ab-ac}{ac-bc}$=1����ab-ac=ac-bc��
��ab+bc=2ac��
��abc��0��
��$\frac{1}{a}+\frac{1}{c}=\frac{2}{b}$��
���� ���⿼���˸���ϵ���Ĺ�ϵ�Լ������ʽ������Ĺؼ�����1�����������ʽ��ʾ��x����2��������ϵ����ӵó����̵������ֱ�Ϊ1��$\frac{ab-ac}{ac-bc}$���������ڻ����⣬�ѶȲ������������Ŀʱ�����������ʽ��ʾ�����̵Ľ��ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
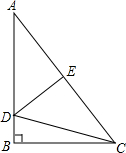 ��ͼ��Rt��ABC�У���B=90�㣬AB=4��BC=3����DE�۵�ʹ��A���C�պ��غϣ���CD�ij�Ϊ$\frac{25}{8}$��
��ͼ��Rt��ABC�У���B=90�㣬AB=4��BC=3����DE�۵�ʹ��A���C�պ��غϣ���CD�ij�Ϊ$\frac{25}{8}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���εĶԽ������ | |
| B�� | ƽ���ı��εĶԽ�����ƽ�� | |
| C�� | �Խ�����ȵ��ı����Ǿ��� | |
| D�� | �Խ����ഹֱƽ�ֵ��ı��������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
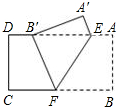 ��ͼ���Ѿ���ֽƬABCD��EF�۵���ʹ��B���ڱ�AD�ϣ��ĵ�B�䴦����A���ڵ�A�䴦����AE=6��BF=10����AB=8��
��ͼ���Ѿ���ֽƬABCD��EF�۵���ʹ��B���ڱ�AD�ϣ��ĵ�B�䴦����A���ڵ�A�䴦����AE=6��BF=10����AB=8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
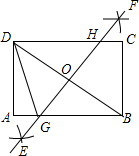 ��ͼ���ھ���ABCD�У���ֱ�ߺ�Բ����BD�Ĵ�ֱƽ����EF����AB�ڵ�G����DC�ڵ�H����AB=4��BC=3����AG�ij�Ϊ��������
��ͼ���ھ���ABCD�У���ֱ�ߺ�Բ����BD�Ĵ�ֱƽ����EF����AB�ڵ�G����DC�ڵ�H����AB=4��BC=3����AG�ij�Ϊ��������| A�� | $\frac{25}{8}$ | B�� | $\frac{7}{4}$ | C�� | $\frac{7}{8}$ | D�� | $\frac{5}{8}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com