D
分析:有条件可直接证得△ACD≌△ACE;有三角形全等的性质可得CD=CE,又因为AD=AE所以AC是DE的垂直平分线即AC垂直平分ED;取CF的中点O连接BO,可得CE=2BO,再证明BF=BO即可,即问题转化为证明△EBC≌△EHC.再利用三角形的外角性质问题③④可得证.
解答:

解:∵AD∥BC,∠ABC=90°,
∴∠BAD=90°.
∵AB=CB,
∴∠BAC=45°,
∴∠DAC=45°.
又∵AC=AC,
∴△AEC≌△ADC.
∴①△ACD≌△ACE正确.
∵△AEC≌△ADC,
∴DC=CE.
又∵AD=AE,
∴AC是DE的垂直平分线.
即AC垂直平分ED.
∴②AC垂直平分ED正确.
易证F、A、B、C共圆,
因为BC为弦,∠CFB=CAB=45°,FB∥CD,
所以∠FCD=45°,∠ACE=∠ACD=22.5°,
又因为∠ACB=45°,
所以∠FCB等于22.5,
故④正确;

延长DA,交BF延长线于M,
易证MBCD是平行四边形,对
角相等,所以∠M=67.5°,
易证∠FAB=∠FCB(以FB为弦,亦可以用8字结构,相似),
所以∠FAE=22.5°,
所以∠MAF=67.5°,
所以∠M=∠MAF,
故AF=MF,
易证∠EBF=22.5°,
所以∠FAB=∠FBA,
所以AF=FB,
所以MF=BF,
又因为MB=CD=CE(对边以及全等),
所以2FB=CE④∵∠ABC=90°,OE=OC,
∴BO=CO=

CE
∴∠OCB=∠OBC.
∵∠FOB=∠OCB+∠OBC,
∴∠FOB=2∠OCB.
∵BF∥CD,
∴∠BFO=∠DCF.
∵∠BFO=∠DCF=∠FOB,
∴∠BFO=∠FOB.
∴BF=OB.
∴BF=

CE,
即CE=2BF,故③正确.
故答案选D.
点评:本题考查了三角形全等的判断和性质;垂直平分线的判定;直角三角形斜边上的中线等于斜边的一半;等腰直角三角形两底角都是45°,题目难度不小,有一定的综合性.

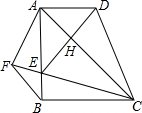 在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,且BF∥CD,AF⊥CE于F.连接DE交对角线AC于H.下列结论:①△ACD≌△ACE;②AC垂直平分ED;③CE=2BF;④CE平分∠ACB.其中结论正确的是
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,且BF∥CD,AF⊥CE于F.连接DE交对角线AC于H.下列结论:①△ACD≌△ACE;②AC垂直平分ED;③CE=2BF;④CE平分∠ACB.其中结论正确的是 解:∵AD∥BC,∠ABC=90°,
解:∵AD∥BC,∠ABC=90°, 延长DA,交BF延长线于M,
延长DA,交BF延长线于M, CE
CE CE,
CE,

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案