
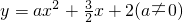 的图象与x轴交于A、B两点,与y轴交于C点我,已知B点坐标(4,0).
的图象与x轴交于A、B两点,与y轴交于C点我,已知B点坐标(4,0).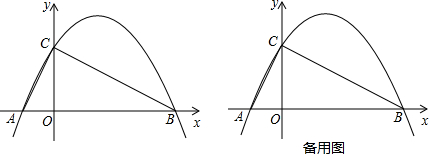
 ,
, a2+
a2+ x+2.
x+2. x2+
x2+ x+2,
x+2, ,0).
,0).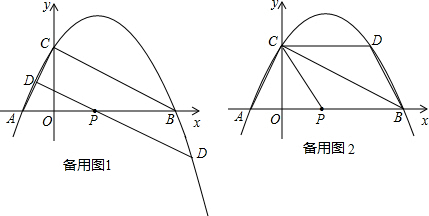
 ,
,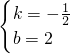 ,
, +2,
+2, x+c,
x+c, ,0)代入可得:-
,0)代入可得:- ×
× +c=0,
+c=0, ,
, x+
x+ ,
,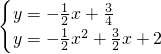 ,
,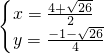 或
或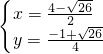 ,
,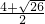 ,
,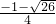 )或(
)或(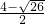 ,
,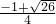 ).
).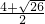 ,
,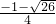 )或(
)或(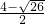 ,
,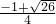 )或(3,2).
)或(3,2).

科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 3 |

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏响水县教研片九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,抛物线 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
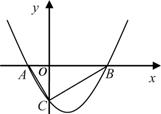
(1)求抛物线的解析式;
(2)判断△ABC的形状,说出△ABC外接圆的圆心位置,并求出圆心的坐标.
查看答案和解析>>
科目:初中数学 来源:2013年湖北省中考数学预测试卷(解析版) 题型:解答题
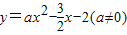 的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).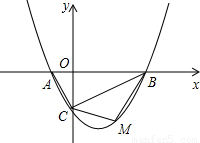
查看答案和解析>>
科目:初中数学 来源:2013年广东省深圳市育才二中中考数学一模试卷(解析版) 题型:解答题
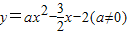 的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省盐城市滨海县九年级下学期期末调研数学试卷(解析版) 题型:解答题
如图,抛物线 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
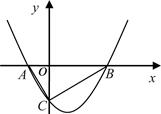
(1)求抛物线的解析式;
(2)判断△ABC的形状,说出△ABC外接圆的圆心位置,并求出圆心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com