
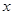 轴交于点
轴交于点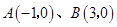 两点,与
两点,与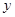 轴交于点
轴交于点 以
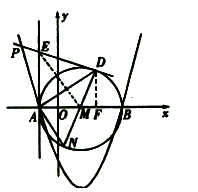
以 为直径作
为直径作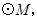 过抛物线上一点
过抛物线上一点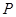 作
作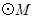 的切线
的切线 切点为
切点为 并与
并与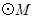 的切线
的切线 相交于点
相交于点 连结
连结 并延长交
并延长交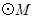 于点
于点 连结
连结

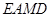 的面积为
的面积为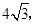 求直线
求直线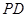 的函数关系式;
的函数关系式;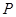 ,使得四边形
,使得四边形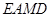 的面积等于
的面积等于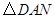 的面积?若存在,求出点
的面积?若存在,求出点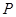 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. 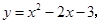 ,
,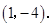 (2)
(2)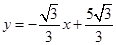 或
或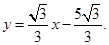 (3)
(3)
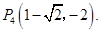
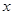 轴交于点
轴交于点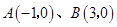 两点,设抛物线的函数关系式为:
两点,设抛物线的函数关系式为: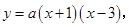
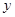 轴交于点
轴交于点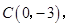
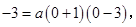
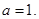
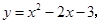 ················· 2分
················· 2分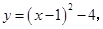
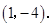 ······················ 3分
······················ 3分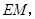
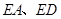 是
是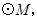 的两条切线,
的两条切线,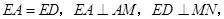 ∴
∴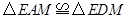
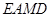 的面积为
的面积为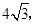 ∴
∴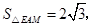 ∴
∴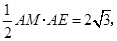
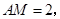 ∴
∴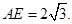
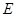 的坐标为
的坐标为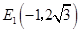 或
或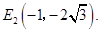 ··············· 5分
··············· 5分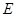 点在第二象限时,切点
点在第二象限时,切点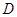 在第一象限.
在第一象限.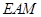 中,
中,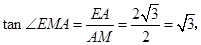
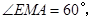 ∴
∴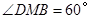
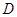 作
作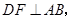 垂足为点
垂足为点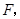
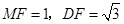
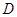 的坐标为
的坐标为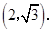 ························ 6分
························ 6分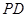 的函数关系式为
的函数关系式为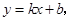 将
将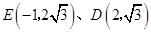 的坐标代入得
的坐标代入得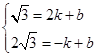 解之,得
解之,得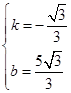
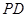 的函数关系式为
的函数关系式为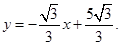 ··············· 7分
··············· 7分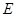 点在第三象限时,切点
点在第三象限时,切点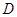 在第四象限.
在第四象限.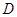 的坐标为
的坐标为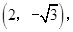 直线
直线 的函数关系式为
的函数关系式为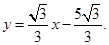
 的函数关系式为
的函数关系式为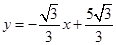 或
或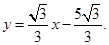 ····················· 8分
····················· 8分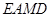 的面积等于
的面积等于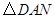 的面积
的面积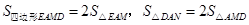
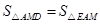
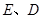 两点到
两点到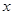 轴的距离相等,
轴的距离相等,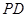 与
与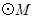 相切,∴点
相切,∴点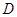 与点
与点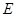 在
在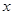 轴同侧,
轴同侧,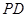 与
与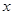 轴平行,
轴平行,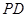 的函数关系式为
的函数关系式为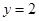 或
或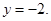
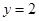 时,由
时,由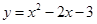 得,
得,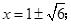
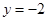 时,由
时,由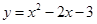 得,
得,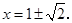 ················ 11分
················ 11分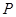 的位置有4个,分别是
的位置有4个,分别是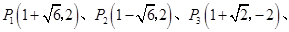
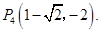 ······························ 12分
······························ 12分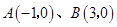 ,
,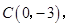 求得抛物线的函数关系式和顶点坐标
求得抛物线的函数关系式和顶点坐标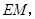 通过
通过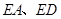 是
是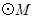 的两条切线,得到
的两条切线,得到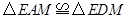 ,通过四边形
,通过四边形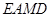 的面积和
的面积和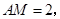 得到
得到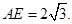 ,从而求得E点坐标有两个,分别求得切点
,从而求得E点坐标有两个,分别求得切点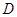 的坐标,求得直线
的坐标,求得直线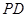 的函数关系式
的函数关系式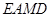 的面积等于
的面积等于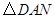 的面积,即
的面积,即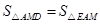 ,得出切线
,得出切线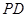 与
与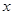 轴平行,通过切线
轴平行,通过切线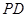 的函数关系式,求得点
的函数关系式,求得点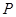 的坐标
的坐标

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
 的坐标分别为
的坐标分别为 .
. ,使得
,使得 与
与 关于点
关于点 成中心对称;
成中心对称; 的三个顶点,求此二次函数的关系式.
的三个顶点,求此二次函数的关系式.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
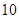 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产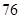 件,每件利润
件,每件利润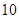 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加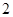 元.
元. 元时,此产品质量在第几档次?
元时,此产品质量在第几档次? 件.若生产第
件.若生产第 档的产品一天的总利润为
档的产品一天的总利润为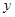 元(其中
元(其中 为正整数,且
为正整数,且 ≤
≤ ≤
≤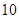 ),求出
),求出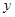 关于
关于 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线
的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线 始终有公共点,请在图一中作出这样的公共点。
始终有公共点,请在图一中作出这样的公共点。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图像与
的图像与 轴相交于点A、B,顶点为C,点D在这个二次函数图像的对称轴上,若四边形ABCD时一个边长为2且有一个内角为60°的菱形,求此二次函数的表达式。
轴相交于点A、B,顶点为C,点D在这个二次函数图像的对称轴上,若四边形ABCD时一个边长为2且有一个内角为60°的菱形,求此二次函数的表达式。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com