市政府要求武汉轻轨二七路段工程12个月完工.现由甲、乙两工程队参与施工,已知甲队单独完成需要16个月,每月需费用600万元;乙队单独完成需要24个月,每月需费用400万元.由于前期工程路面较宽,可由甲、乙两队共同施工.随着工程的进行,路面变窄,两队再同时施工,对交通影响较大,为了减小对解放大道的交通秩序的影响,后期只能由一个工程队施工.工程总指挥部结合实际情况现拟定两套工程方案:
①先由甲、乙两个工程队合做m个月后,再由甲队单独施工,保证恰好按时完成.
②先由甲、乙两个工程队合做n个月后,再由乙队单独施工,也保证恰好按时完成.
(1)求两套方案中m和n的值;
(2)通过计算,并结合施工费用及施工对交通的影响,你认为该工程总指挥部应该选择哪种方案?
解:(1)由①得:
(

+

)m+

(12-m)=1,
解得:m=6,
由②得:
(

+

)n+

(12-n)=1,
解得:n=8;
(2)由(1)得第①个方案:甲工程队作6+(12-6)=12个月,乙工程队作6个月,
则总费用为:600×12+400×6=9600(万元),
第②个方案:甲工程队作8个月,乙工程队作8+(12-8)=12个月,
则总费用为:600×8+400×12=9600(万元),
因为费用两个方案相同,但考虑进度第一个方案优于第二个方案.
分析:(1)设总工程量为“1”,则甲工程队每个月完成

,乙工程队完成

,根据①②两种情况列出关于m、n的一元一次方程求解.
(2)由(1)求出①②两个方案的施工费用,得出该工程总指挥部应该选择哪种方案.
点评:此题考查的知识点是一元一次方程的应用,关键是根据两种情况列方程求解,再计算出两种情况的费用进行选择.

 +
+ )m+
)m+ (12-m)=1,
(12-m)=1, +
+ )n+
)n+ (12-n)=1,
(12-n)=1, ,乙工程队完成
,乙工程队完成 ,根据①②两种情况列出关于m、n的一元一次方程求解.
,根据①②两种情况列出关于m、n的一元一次方程求解.

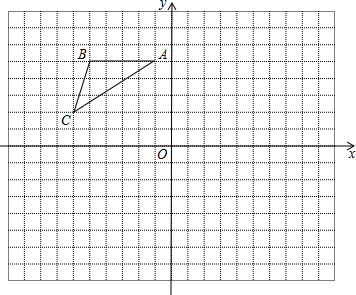 已知△ABC的顶点坐标是A(-1,5),B(-5,5),C(-6,2)
已知△ABC的顶点坐标是A(-1,5),B(-5,5),C(-6,2) ;
;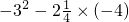 ]÷(
]÷(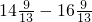 );
);