分析:若a与b相等,直接求出所求式子的值;若a与b不相等,根据题中已知的ax02+bx0+c=0(a≠0),则x0是一元二次方程ax2+bx+c=0的一根,由实数a、b满足a2+3a-1=0,b2+3b-1=0,得到a与b为一个一元二次方程的两根,找出此方程中的a,b及c,计算出b2-4ac,发现其值大于0,故利用根与系数的关系求出两根之和与两根之积,然后把所求式子通分后,分子配方得到关于a+b与ab的式子,将a+b与ab的值整体代入即可求出值.
解答:解:当a=b时,
+=1+1=2;
当a≠b时,a与b为方程x
2+3x-1=0的两个根,
∵a=1,b=3,c=-1,
∴b
2-4ac=3
2+4=13>0,
由根与系数的关系得:a+b=-
=-3,ab=
=-1,
∴
+=
===-11.
综上,
+的值为2或-11.
点评:此题考查了根与系数的关系,在运用根与系数关系时,先考虑一元二次方程中根的判别式大于等于0,即方程有解这个前提,然后利用通分、配方、提取公因式等方法把所求的式子变形为与两根之和及两根之积有关的式子,最后把求出的两根之和与两根之积整体代入即可求出值.本题分两种情况考虑:a与b相等;a与b不相等,学生做题时考虑问题要全面,不要遗漏解.



 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案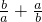 的值.
的值.