
【题目】用适当的方法解下列方程:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
【答案】(1) ![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)用公式法求解即可;
(2)将等号右边移至左边,提出公因式(x-2),利用因式分解法求解;
(3)将等号右边移至左边,利用平方差公式分解因式,利用因式分解法求解.
试题解析:
解:(1)x2-5x+1=0,
a=1,b=-5,c=1,
∴x=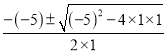 =
=![]() ;
;
(2)3(x-2)2=x(x-2)
3(x-2)2-x(x-2)=0
(x-2)(2x-6)=0
∴x-2=0或2x-6=0
∴x1=2,x2=3;
(3)(y+2)2=(3y-1)2
(y+2)2-(3y-1)2=0
[(y+2)+(3y-1)][ (y+2)-(3y-1)]=0
(4y+1)(-2y+3)=0
∴4y+1=0或-2y+3=0
∴y=![]() 或y=
或y=![]() .
.
点睛: 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() 为边
为边![]() 的中点.
的中点. ![]() 是
是![]() 上一点,⊙
上一点,⊙![]() 与
与![]() 相切于点
相切于点![]() ,且与
,且与![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() .连接
.连接![]() 交
交![]() 于点
于点![]() .
.

(![]() )求证:
)求证: ![]() .
.
(![]() )已知
)已知![]() ,
, ![]() .当
.当![]() 是⊙
是⊙![]() 的直径时,求
的直径时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
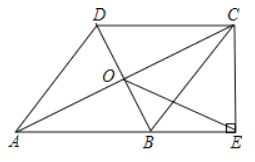
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)如图2,在(1)的条件下,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
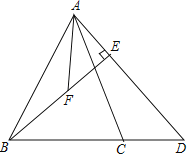
【题目】如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
(1)若AC=![]() ,AE=
,AE=![]() ,求BE的长;
,求BE的长;
(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.
(3)若∠BAC=∠DAF,求证:2AF=AD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年汶川车厘子喜获丰收,车厘子一上市,水果店的王老板用2500元购进一批车厘子,很快售完;老板又用4400元购进第二批车厘子,所购数量是第一批的2倍,由于进货量增加,进价比第一批每干克少了3元.”
(l)第一批车厘子每千克进价多少元?.
(2)该老板在销售第二批车厘子时,售价在第二批进价的基础上增加了![]() ,售出
,售出![]() 后,为了尽快售完,决定将剩余车厘子在第二批进价的基础上每千克降价
后,为了尽快售完,决定将剩余车厘子在第二批进价的基础上每千克降价![]() 元进行促销,结果第二批车厘子的销售利润为1520元,求
元进行促销,结果第二批车厘子的销售利润为1520元,求![]() 的值。(利润=售价一进价)
的值。(利润=售价一进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庆元大道两侧需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
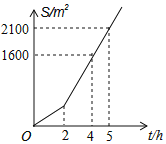
A. 200B. 300C. 400D. 500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,CE是∠DCB的平分线,F是AB的中点,AB=6,BC=5,则AE:EF:FB为( )

A. 1:2:3 B. 2:1:3 C. 3:2:1 D. 3:1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
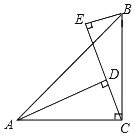
【题目】已知:如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E.
(1)求证:△BEC≌△CDA;
(2)当AD=3,BE=1时,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com