
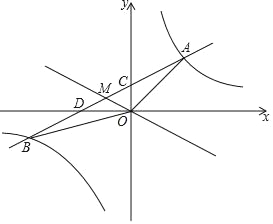
【题目】如图,一次函数y=kx+1与反比例函数y=![]() (m≠0)相交于A、B两点,与x轴,y轴分别交于D、C两点,已知sin∠CDO=
(m≠0)相交于A、B两点,与x轴,y轴分别交于D、C两点,已知sin∠CDO=![]() ,△BOD的面积为1.
,△BOD的面积为1.
(1)求一次函数和反比例函数的解析式;
(2)连接OA,OB,点M是线段AB的中点,直线OM向上平移h(h>0)个单位将△AOB的面积分成1:7两部分,求h的值.
【答案】(1)y=![]() ;(2)h=
;(2)h=![]() .
.
【解析】
(1)解直角三角形求出点D坐标,再利用三角形的面积公式求出点B坐标即可解决问题;
(2)设平移后的中交OA于G,交AC于H.利用方程组求出点A坐标,利用中点坐标公式求出点M坐标,求出直线OM的解析式,再证明S△AHG:S△AOM=1:4,推出AG:AO=1:2,推出GA=OG,可得G(1,1),求出直线GH的解析式即可解决问题;
解:(1)由题意点C(0,1),
在Rt△ODC中,∵OC=1,sin∠CDO=![]() ,
,
∴OD=2,
∴D(﹣2,0),
把D(﹣2,0)代入y=kx+1,得到k=![]() ,
,
∴一次函数的解析式为y=![]() x+1,
x+1,
∵△BOD的面积为1,设B(x,y),
∴![]() ×2×|y|=1,
×2×|y|=1,
∵y<0,
∴y=﹣1,
∴B(﹣4,﹣1),
∴m=4,
∴反比例函数的解析式为y=![]() .
.
(2)设平移后的中交OA于G,交AC于H.
由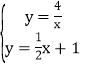 ,解得
,解得![]() 或
或![]() ,
,
∴A(2,2),∵B(﹣4,﹣1),
∴M(﹣1,![]() ),
),
∴直线OM的解析式为y=﹣![]() x,
x,
∵AM=MB,
∴S△AMO=S△BMO,
∵S△AHG:S四边形OBHG=1:7,
∴S△AHG:S△AOM=1:4,
∴AG:AO=1:2,
∴GA=OG,
∴G(1,1),
∴直线HG的解析式为y=﹣![]() x+
x+![]() ,
,
∴h=![]() .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买![]() 种图书花费了3000元,购买
种图书花费了3000元,购买![]() 种图书花费了1600元,A种图书的单价是
种图书花费了1600元,A种图书的单价是![]() 种图书的1.5倍,购买
种图书的1.5倍,购买![]() 种图书的数量比
种图书的数量比![]() 种图书多20本.
种图书多20本.
(1)求![]() 和
和![]() 两种图书的单价;
两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了![]() 种图书20本和
种图书20本和![]() 种图书25本,共花费多少元?
种图书25本,共花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
(1)求证:PB是的切线.
(2)若PB=6,DB=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
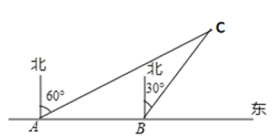
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实行常态化巡航管理,如图,正在执行巡航任务的海监船以每小时30海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东60°方向上, 继续航行
在北偏东60°方向上, 继续航行![]() 后到达
后到达![]() 处, 此时测得灯塔
处, 此时测得灯塔![]() 在北偏东30°方向上.
在北偏东30°方向上.
(1) 求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围15海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围15海里内有暗礁,问海监船继续向正东方向航行是否安全?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
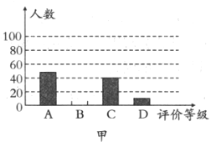
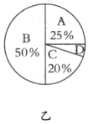
【题目】学校为了调查学生对教学的满意度,随机抽取了部分学生作问卷调查:用“![]() ”表示“很满意”,“
”表示“很满意”,“![]() ”表示“满意”,“
”表示“满意”,“![]() ”表示“比较满意”,“
”表示“比较满意”,“![]() ”表示“不满意”,下图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
”表示“不满意”,下图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了多少名学生?
(2)将图甲中“![]() ”部分的图形补充完整;
”部分的图形补充完整;
(3)求出图乙中扇形![]() 的圆心角的度数.
的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
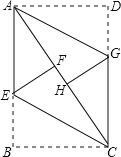
【题目】如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形:
(2)若AB=8cm,BC=6cm,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).

(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(记过保留根号和π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com