
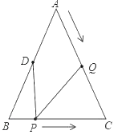
【题目】如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C 以4cm/s的速度运动.若点P、Q两点分别从点B、A同时出发.
(1)经过2秒后,求证:∠DPQ=∠C.
(2)若△CPQ的周长为18cm,问经过几秒钟后,△CPQ是等腰三角形?
【答案】(1)见解析;(2)经过1秒或![]() 秒或
秒或![]() 秒时,△CPQ是等腰三角形.
秒时,△CPQ是等腰三角形.
【解析】
(1)经过1秒后,PB=2m,PC=8m,CQ=6m,由已知可得BD=PC,BP=CQ,∠ABC=∠ACB,即据SAS可证得△BPD≌△CQP,然后根据全等三角形的性质及三角形外角的性质即可解答;
(2)可设点Q的运动时间为ts△CPQ是等腰三角形,则可知PB=2tcm,PC=8-3tcm,CQ=xtcm,据(1)同理可得当BD=PC,BP=CQ或BD=CQ,BP=PC时△CPQ为等腰三角形,从而求得t的值.
(1)当P,Q两点分别从B,A两点同时出发运动2秒时,
有BP=2×2=4cm,AQ=4×2=8cm,则CP=BC﹣BP=10﹣4=6cm,
CQ=AC﹣AQ=12﹣8=4cm,∵D是AB的中点,
∴BD=![]() AB=
AB=![]() ×12=6cm,
×12=6cm,
∴BP=CQ,BD=CP,
又∵△ABC中,AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,
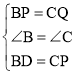 ,
,
∴△BPD≌△CQP(SAS)
∴∠DPB=∠PQC,
∵∠B+∠PDB=∠DPQ+∠QPC,
∴∠DPQ=∠C;
(2)设当P,Q两点同时出发运动t秒时,
有BP=2t,AQ=4t
∴t的取值范围为0<t≤3,
则CP=10﹣2t,CQ=12﹣4t,
∵△CPQ的周长为18cm,
∴PQ=18﹣(10﹣2t)﹣( 12﹣4t)=6t﹣4,
要使△CPQ是等腰三角形,则可分为三种情况讨论:
①当CP=CQ时,则有10﹣2t=12﹣4t,
解得:t=1.
②当PQ=PC时,则有6t﹣4=10﹣2t,
解得:t=![]() ;
;
③当QP=QC时,则有6t﹣4=12﹣4t,
解得:t=![]() ,
,
三种情况均符合t的取值范围.
综上所述,经过1秒或![]() 秒或
秒或![]() 秒时,△CPQ是等腰三角形.
秒时,△CPQ是等腰三角形.


科目:初中数学 来源: 题型:
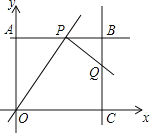
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.
(1)求点B的坐标;
(2)当点P在线段AB上运动(不与A,B重合)时,设点P的横坐标为m,线段CQ的长度为l.求出l关于m的函数解析式;
(3)在坐标平面内是否存在点D,使以O、P、Q、D为顶点的四边形为正方形?若存在,请直接写出D点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
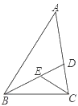
【题目】①如图,在△ABC中,∠A=55°,∠ABD=32°,∠ACB=70°,且CE平分∠ACB,求∠DEC的度数.
②先化简再求值:化简:![]() ,x=2020.
,x=2020.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,E为CA延长线上一点,D为AB上一点,F为
,E为CA延长线上一点,D为AB上一点,F为![]() 外一点且
外一点且![]() 连接DF,BF.
连接DF,BF.
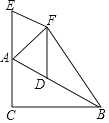
(1)当![]() 的度数是多少时,四边形ADFE为菱形,请说明理由:
的度数是多少时,四边形ADFE为菱形,请说明理由:
(2)当AB= 时,四边形ACBF为正方形(请直接写出)
查看答案和解析>>
科目:初中数学 来源: 题型:
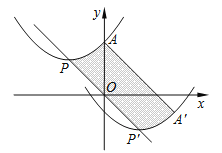
【题目】如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD是正方形,点E、F分别在线段BC、DC上,∠BAE=30°.若线段AE绕点A逆时针旋转后与线段AF重合,则旋转的角度是( )

A.30°B.45°C.60°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,∠AOC=30°,点C在AB的上方.MON为直角三角板,O为直角顶点,![]() ,ON在射线OC上.将三角板MON绕点O以每秒6°的速度沿逆时针方向旋转,与此同时,射线OC绕点O以每秒11°的速度沿逆时针方向旋转,当射线OC与射线OA重合时,所有运动都停止.设运动的时间为t秒,
,ON在射线OC上.将三角板MON绕点O以每秒6°的速度沿逆时针方向旋转,与此同时,射线OC绕点O以每秒11°的速度沿逆时针方向旋转,当射线OC与射线OA重合时,所有运动都停止.设运动的时间为t秒,
(1)旋转开始前,∠MOC= °,∠BOM= °;
(2)运动t秒时,OM转动了 °,t为 秒时,OC与OM重合;
(3)t为何值时,∠MOC=35°?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com