
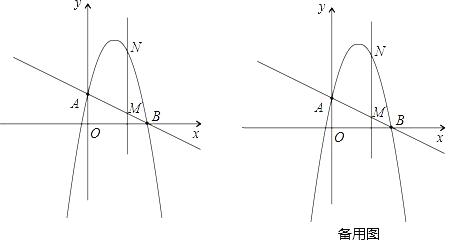
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
【答案】(1)y=x+![]() x+2;(2)t=2时,MN有最大值4;(3)(0,6),(0,2)或(4,4).
x+2;(2)t=2时,MN有最大值4;(3)(0,6),(0,2)或(4,4).
【解析】试题分析:
(1)先由直线![]() 分别交y轴、x轴于点A、B这一条件求出点A、B的坐标,将所求坐标代入抛物线
分别交y轴、x轴于点A、B这一条件求出点A、B的坐标,将所求坐标代入抛物线![]() 列出关于
列出关于![]() 的值即可得到所求抛物线的解析式;
的值即可得到所求抛物线的解析式;
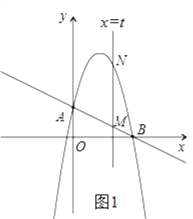
(2)如图1,由题意可知点M的横坐标为t,根据点M在直线![]() 上,点N在(1)中所求抛物线上,可用含“t”的代数式表达出点M、N的坐标,结合第一象限中,点N在点M的上方,可用含“t”的代数式表达出MN的长,把所得式子配方,即可得到所求答案;
上,点N在(1)中所求抛物线上,可用含“t”的代数式表达出点M、N的坐标,结合第一象限中,点N在点M的上方,可用含“t”的代数式表达出MN的长,把所得式子配方,即可得到所求答案;
(3)由(2)中答案可得求得对应的点A、M、N的坐标,如图2分析可知点D有三种可能,其中两种情况点D在y轴上,结合AD=MN,即可求得两个符合要求的点D1、D2的坐标;由图可知第三个符合要求点D就是直线D1N和D2M的交点,求出两直线的解析式联立成方程组,解方程组即可求得第三个符合要求的点D的坐标.
试题解析:
(1)∵![]() 分别交y轴、x轴于A.、B两点,
分别交y轴、x轴于A.、B两点,
∴A、B点的坐标为:A(0,2),B(4,0),
将x=0,y=2代入y=x+bx+c得c=2,
将x=4,y=0,c=2代入y=x+bx+c得0=16+4b+2,解得b=![]() ,
,
∴抛物线解析式为: ![]() ,
,
(2)如图1,由题意可知,直线MN即是直线![]() ,
,
∵点M在直线![]() 上,点N在抛物线
上,点N在抛物线![]() 上,
上,
∴点M、N的坐标分别为![]() 、
、![]() ,
,
∵在第一象限中,点N在点M的上方,
∴MN=![]() ,
,
∴当![]() 时,MN最长=4;
时,MN最长=4;
(3)由(2)可知,A(0,2),M(2,1),N(2,5).
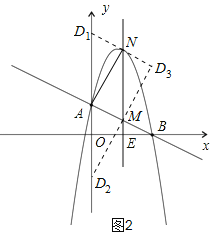
以A. M、N、D为顶点作平行四边形,D点的可能位置有三种情形,如图2所示:
(i)当D在y轴上时,设D的坐标为(0,a)
由AD=MN,得|a2|=4,解得a1=6,a2=2,
从而D1为(0,6)或D2(0,2),
(ii)当D不在y轴上时,由图可知D3为D1N与D2M的交点,
由D1、D2、M、N的坐标可求得直线D1N的解析式为:y=![]() x+6,直线D2M的解析式为:y=
x+6,直线D2M的解析式为:y=![]() x2,
x2,
由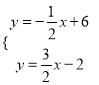 解得
解得![]() ,
,
∴D3的坐标为:(4,4),
综上所述,所求的D点坐标为(0,6),(0,2)或(4,4).


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.

(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票价格如下表所示:

某中学七年级(1)、(2)两个班计划去游览该公园,其中(I)班的人数较少,不足 50 人;(2) 班人数略多,有 50 多人.如果两个班都以班为单位分别购票,则一共应付 1172 元,如 果两个班联合起来,作为一个团体购票,则需付 1078 元.
(1)列方程求出两个班各有多少学生;
(2)如果两个班联合起来买票,是否可以买单价为 9 元的票?你有什么省钱的方法来帮 他们买票呢?请给出最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的点(不与点B,C重合),连结AD

(1)如图1,当点D是BC边上的中点时,则S△ABD:S△ACD=_________(直接写出答案)
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,S△ABD:S△ACD=_________ (用含m,n的代数式表示).
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连结BE,如果AC=2,AB=4,S△BDE =6,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD.
(1)若AB=2,OD=3,求BC的长;
(2)若作直线CD,试说明直线CD是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
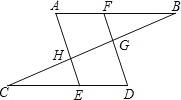
【题目】已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC与H,G,∠A=∠D,∠FGB+∠EHG=180°.
(1)求证:AB∥CD;
(2)若AE⊥BC,直接写出图中所有与∠C互余的角,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1、P2、P3、P4、P5是△DEF边上的5个格点,请按要求完成下列各题:
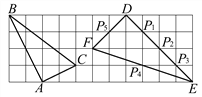
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)直接写出一个与△ABC相似的三角形,使它的三个顶点为P1、P2、P3、P4、P5中的三个格点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.

(1)写出商场销售这种工具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com