
【题目】如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为9cm,则FG=_____cm.

【答案】![]()
【解析】
作GM⊥AC′于M,A′N⊥AD于N,AA′交EC′于K.易知MG=AB=AC′=4.5,首先证明△AKC′≌△GFM,可得GF=AK,由AN=6cm,A′N=3cm,C′K∥A′N,推出![]() ,可得
,可得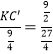 ,得出C′K=2cm,在Rt△AC′K中,根据AK=
,得出C′K=2cm,在Rt△AC′K中,根据AK=![]() ,求出AK即可解决问题.
,求出AK即可解决问题.
解:作GM⊥AC′于M,A′N⊥AD于N,AA′交EC′于K.易知MG=AB=AC′,

∵GF⊥AA′,
∴∠AFG+∠FAK=90°,∠MGF+∠MFG=90°,
∴∠MGF=∠KAC′,
∴△AKC′≌△GFM,
∴GF=AK,
∵AN=![]() cm,A′N=
cm,A′N=![]() cm,C′K∥A′N,
cm,C′K∥A′N,
∴![]() ,
,
∴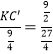 ,
,
∴C′K=1.5cm,
在Rt△AC′K中,AK=![]() =
=![]() =
=![]() cm,
cm,
∴FG=AK=![]() cm,
cm,
故答案为![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
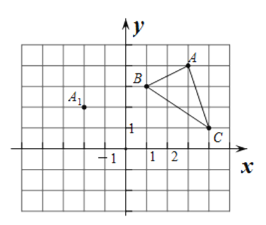
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A的坐标是(3,4),点A1的坐标是(-2,2),现将△ABC平移,使点A平移到A1,点B,C的对应点分别是B1,C1.
(1)请画出平移后的△A1B1C1(不写画法),并直接写出点B1,C1的坐标;
(2)若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标为( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月14日川航3U863航班挡风玻璃在高空爆裂,机组临危不乱,果断应对,正确处置,顺利返航,避免了一场灾难的发生,创造了世界航空史上的奇迹!下表给出了距离地面高度与所在位置的温度之间的大致关系.根据下表,请回答以下几个问题:
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
所在位置的温度(℃) | 20 | 14 | 8 | 2 |
|
(1)上表反映的两个变量中,______是自变量,______是因变量.
(2)若用h表示距离地面的高度,用y表示表示温度,则y与h的之间的关系式是:__________;
当距离地面高度5千米时,所在位置的温度为:_________℃.
如图是当日飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用时间关系图.根据图象回答以下问题:
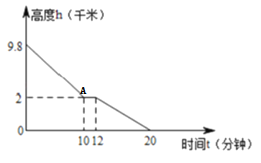
(3)点A表示的意义是什么?返回途中飞机在2千米高空水平大约盘旋了几分钟?
(4)飞机发生事故时所在高空的温度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 和直线
和直线![]() 互相垂直,垂足为
互相垂直,垂足为![]() ,直线
,直线![]() 于点B,E是线段AB上一定点,D为线段OB上的一动点(点D不与点O、B重合),
于点B,E是线段AB上一定点,D为线段OB上的一动点(点D不与点O、B重合),![]() 直
直![]() 于点
于点![]() ,连接AC.
,连接AC.

(1)当![]() ,则
,则![]() ___________°;
___________°;
(2)当![]() 时,请判断CD与AC的位置关系,并说明理由;
时,请判断CD与AC的位置关系,并说明理由;
(3)若![]() 、
、![]() 的角平分线的交点为P,当点D在线段
的角平分线的交点为P,当点D在线段![]() 上运动时,问
上运动时,问![]() 的大小是否会发生变化?若不变,求出
的大小是否会发生变化?若不变,求出![]() 的大小,并说明理由;若变化,求其变化范围.
的大小,并说明理由;若变化,求其变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() =
= ![]() =
=![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②请直接写出线段AD,BD,CD之间的等量关系式;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年秋季,长白山土特产喜获丰收,某土特产公司组织10辆汽车装运甲、乙、丙三种土特产去外地销售,按计划10辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满.设装运甲种土特产的汽车有x辆,装运乙种土特产的汽车有y辆,根据下表提供的信息,解答以下问题.

(1)装运丙种土特产的车辆数为(用含x、y的式子表示);
(2)用含x、y的式子表示这10辆汽车共装运土特产的吨数;
(3)求销售完装运的这批土特产后所获得的总利润(用含x、y的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
如图1,已知△ABC为等边三角形,点D,E分别在边AB、AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:在图1中,线段PM与PN的数量关系是 ,∠MPN的度数是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,
①判断△PMN的形状,并说明理由;
②求∠MPN的度数;
(3)拓展延伸:若△ABC为直角三角形,∠BAC=90°,AB=AC=10,点DE分别在边AB,AC上,AD=AE=4,连接DC,点M,P,N分别为DE,DC,BC的中点.把△ADE绕点A在平面内自由旋转,如图3,请直接写出△PMN面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com