Question

【题目】如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB中点，连接DF、EF、DE、EF与AC交于点O，DE与交于点G，连接OG，若，下列结论：①；②；③EF⊥AC；④．其中正确的结论的序号是___________．

Answer 1

【答案】①③④

【解析】

根据等边三角形的性质求出∠EAC=60°，AE=AC，求出BC=AF，根据SAS证△ABC≌△EFA，推出FE=AB，∠AEF=∠BAC=30°，求出∠AOE=90°，即可判断③；求出AD=BD，BF=AF，∠DFB=∠EAF，∠BDF=∠AEF，根据AAS证△DBF≌△EFA，即可判断①；得出四边形ADFE为平行四边形，推出AG=AF，AG=AB，求出AD=AB，推出AD=4AG，即可判断④；求出∠FAE=90°，∠AFE＜90°，推出EF＞AE，即可判断②．

∵△ACE是等边三角形

∴

∵

∴

∵F为AB的中点

∴

∴

在△ABC和△EFA中

∴

∴，

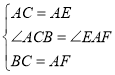
∴，故③正确

∵

∴

∵

∴

∵

∴

∴

在△DBF和△EFA中

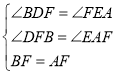
∴，故①正确

∴

∵

∴四边形ADFE为平行四边形

∴

∵

∴，故④正确

∵四边形ADFE为平行四边形

∴

∵

∴

∴，故②错误

正确的有①③④

故答案为：①③④．