
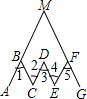
 完成推理填空
完成推理填空分析 延长CD,与MG相交于点N,由∠1=∠2可得出AM∥CN,故可得出∠AMG=∠CNG,再由∠4=∠5得出MG∥DE,据此得出∠CNG=∠3,进而可得出结论.
解答  解:∠AMG=∠3.
解:∠AMG=∠3.
理由:延长CD,与MG相交于点N.
∵∠1=∠2(已知),
∴AM∥CN(内错角相等,两直线平行),
∴∠AMG=∠CNG,(两直线平行,同位角相等).
∵∠4=∠5(已知)
∴MG∥DE.,
∴∠CNG=∠3,
∴∠AMG=∠3.
故答案为:AM,CN,内错角相等,两直线平行∠CNG,两直线平行,同位角相等;MG,DE;CNG.
点评 本题考查的是平行线的判定与性质,根据题意作出辅助线,构造出平行线是解答此题的关键.


科目:初中数学 来源: 题型:解答题
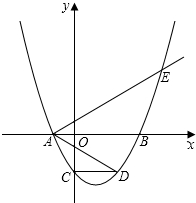 如图,抛物线y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)与x轴分别交于点A(x1,0),B(x2,0)(点A位于点B的左侧),与y轴交于点C(0,-3),
如图,抛物线y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)与x轴分别交于点A(x1,0),B(x2,0)(点A位于点B的左侧),与y轴交于点C(0,-3),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
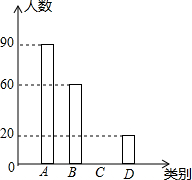 雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:
雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:| 类别 | 雾霾天气的主要成因 | 百分比 |
| A | 工业污染 | 45% |
| B | 汽车尾气排放 | m |
| C | 城中村燃煤问题 | 15% |
| D | 其他(绿化不足等) | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
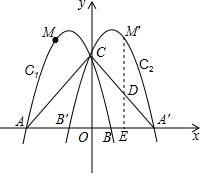 如图,抛物线C1:y=ax2+bx+4与x轴交于A(-3,0),B两点,与y轴交于点C,点M(-$\frac{3}{2}$,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
如图,抛物线C1:y=ax2+bx+4与x轴交于A(-3,0),B两点,与y轴交于点C,点M(-$\frac{3}{2}$,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com