
【题目】一辆出租车司机某天在东西方向的公路上营运,往东行驶的路程记作正数,往西行驶的路程记作负数.全天行程的记录如下:30,-28,-13,15,27,-30,45,-27;(单位:千米)
(1)当小张将最后一位乘客送到目的地时,距出发地点的距离为多少千米?
(2)若每千米的营业额为7元,则小张这天的总营业额为多少元?
(3)在(2)的情况下,如果营运成本为每千米2元,那么这天盈利多少元?
【答案】(1) 当小张将最后一位乘客送到目的地时,距出发地点的距离为19千米; (2) 若每千米的营业额为7元,则小张这天的总营业额为1505元;(3) 在(2)的情况下,如果营运成本为每千米2元,那么这天盈利1075元
【解析】
(1)根据有理数的加法,可得答案;
(2)根据单价乘以路程,可得营业额;
(3)根据路程乘以每千米的盈利,可得答案.
(1)![]()
![]()
![]()
![]() 千米,
千米,
答:当小张将最后一位乘客送到目的地时,距出发地点的距离为19千米;
(2)![]()
![]()
![]()
![]() (元),
(元),
答:若每千米的营业额为7元,则小张这天的总营业额为1505元;
(3)![]()
![]()
![]() (元),
(元),
答:在(2)的情况下,如果营运成本为每千米2元,那么这天盈利1075元.


科目:初中数学 来源: 题型:
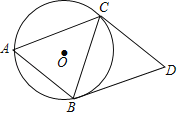
【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=![]() ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
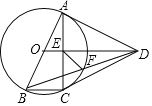
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图:
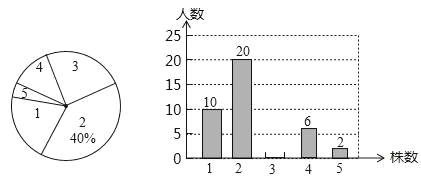
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)扇形统计图中植树为1株的扇形圆心角的度数为 ;
(3)该班同学植树株数的中位数是
(4)小明以下方法计算出该班同学平均植树的株数是:(1+2+3+4+5)÷5=3(株),根据你所学的统计知识
判断小明的计算是否正确,若不正确,请写出正确的算式,并计算出结果
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂销售一种茶壶和茶杯,茶壶每只定价40元,茶怀每只定价5元.厂方在开展促销活动期间,向客户提供两种优惠方案:①茶壶和茶杯都按定价的90%付款;②买一个茶壶送一个茶杯.现某客户要到该厂购买![]() 个茶壶(
个茶壶(![]() ),茶杯个数是茶壶数的4倍少5.
),茶杯个数是茶壶数的4倍少5.
(1)若该客户按方案①购买,需付款______元(用含![]() 的代数式表示);若该客户按方案②购买.需付款______元;(用含
的代数式表示);若该客户按方案②购买.需付款______元;(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
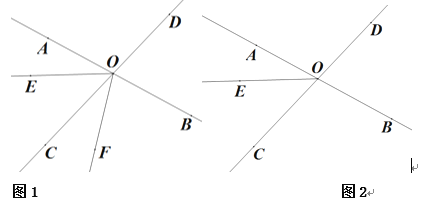
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE=![]() ∠EOC
∠EOC
(1)求∠AOE的度数;
(2)将射线OE绕点O逆时针旋转![]() °(0°<α<360°)到OF.
°(0°<α<360°)到OF.
①如图2,当OF平分∠BOE时,求∠DOF的度数;
②若∠AOF=120°时,直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(![]() ,
,![]() m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应大括号里:![]() ,
,![]() 、-(-10) 、 -(-2)2,0.1010010001…
、-(-10) 、 -(-2)2,0.1010010001…
(1)正数集合{ …}
(2)整数集合{ …}
(3)正分数集合{ …}
(4)非负整数集合{ …}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com