练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图：用一段长为30m的篱笆围成一边靠墙的矩形菜园，墙长为18m，设菜园的宽AB为xm，面积为Sm2．
    （1）求S与x的函数关系式；并直接写出自变量x的取值范围；
    （2）这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？

    分析 （1）设菜园的宽AB为xm，则BC为（30-2x）m，由面积公式写出S与x的函数关系式，进而求出x的取值范围；
    （2）利用二次函数求最值的知识可得出菜园的最大面积．

    解答 解：（1）∵AB=CD=xm，
    ∴BC=（30-2x）m，
    由题意得S=x（30-2x）=-2x2+30x（0＜x＜15）；

    （2）∵S=-2x2+30x=-2（x-7.5）2+112.5，
    ∴当x=7.5时，S有最大值，S最大=112.5，
    此时这个矩形的长为15m、宽为7.5m．
    答：这个矩形的长、宽各为15m、7.5m时，菜园的面积最大，最大面积是112.5m2．

    点评 此题主要考查了二次函数的应用，难度一般，应注意配方法求最大值在实际中的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    15．因式分解4x2-4=4（x+1）（x-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．方程组$\left\{\begin{array}{l}{x-y=1}\\{2x+y=5}\end{array}\right.$的解是（　　）
    A．$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$B．$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$C．$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$D．$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

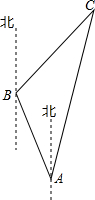    13．为有效开发海洋资源，保护海洋权益，我国对南海诸岛进行了全面调查，一测量船在A岛测得B岛在北偏西30°，C岛在北偏东15°，航行100海里到达B岛，在B岛测得C岛在北偏东45°，求B，C两岛及A，C两岛的距离（$\sqrt{6}$≈2.45，结果保留到整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．
    【问题情境】
    将一副直角三角板（Rt△ABC和Rt△DEF）按图1所示的方式摆放，其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥BC于点N，试判断线段OM与ON的数量关系，并说明理由．
    【探究展示】
    小宇同学展示出如下正确的解法
    解：OM=ON，
    证明如下：
    连接CO，则CO是AB边上的中线
    ∵CA=CB，
    ∴CO是∠ACB的角平分线．（依据1）
    ∵OM⊥AC，ON⊥BC，
    ∴OM=ON（依据2）
    【反思交流】
    （1）上述证明过程中的“依据1”和“依据2”分别是指
    依据1：等腰三角形三线合一（或等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合）
    依据2：角平分线上的点到角的两边距离相等
    （2）你有与小宇不同的思考方法吗？请写出你的证明过程．
    【拓展延伸】
    （3）将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置，使点D落在BA的延长线上，FD的延长线与CA的延长线垂直相交于点M，BC的延长线与DE垂直相交于点N，连接OM，ON，试判断线段OM，ON的数量关系与位置关系，并写出证明过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．甲经销商库存有1200套A品牌服装，每套进价400元，每套售价500元，一年内可卖完．现市场上流行B品牌服装，每套进价300元，每套售价600元，但一年内只允许经销商一次性订购B品牌服装，一年内B品牌服装销售无积压．因甲经销商无流动资金，只有低价转让A品牌服装，用转让来的资金购进B品牌服装，并销售．经与乙经销商协商，甲、乙双方达成转让协议，转让价格y（元/套）与转让数量x（套）之间的函数关系式为y=$-\frac{1}{10}x+360（100≤x≤1200）$．若甲经销商转让x套A品牌服装，一年内所获总利润为w（元）．
    （1）求转让后剩余的A品牌服装的销售款Q1（元）与x（套）之间的函数关系式；
    （2）求B品牌服装的销售款Q2（元）与x（套）之间的函数关系式；
    （3）求w（元）与x（套）之间的函数关系式，并求w的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．如果$\sqrt{{a}^{2}}$-a=b成立，且b＞0，则a取值范围是（　　）
    A．a＜0B．a＞0C．a≥0D．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图1，将矩形OABC放置在平面直角坐标系中，且A（3，0），C（0，3$\sqrt{3}$）．抛物线y=ax2+bx过点B，且与x轴的一个交点为D（6，0）．
    （1）求a，b的值．
    （2）若点P是x轴上方的抛物线上一动点，连接PA，PC，当△PAC面积最大时，求点P的坐标．
    （3）如图2，若线段AB上有一动点，从点B出发，以某一速度匀速运动到某一位置Q处，然后以原来速度的2倍，沿线段QO运动到原点O处．试确定点Q的位置，使得按照上述要求到达原点所用的时间最短．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

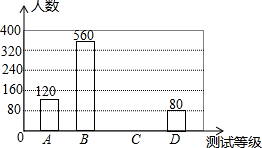    20．某区为了解2016年即将毕业的初中学生的心理状态，围绕“即将中考，你感觉自己的心理状态为：A优、B良、C中、D差（必须选且只选一项）”对全区各个学校随机抽取部分学生进行了问卷调查，在整理调查问卷后绘制成如图所示的不完整的条形统计图，其中选A的学生人数占所调查人数的15%，请你根据以上信息回答下列问题：
    （1）这次调查中，共抽取了学生多少人？
    （2）在这次调查中，选择C的学生人数占所调查的人数的百分比是多少？并补全条形图；
    （3）2016年该区即将毕业的初中学生有4500人，请你估计这些即将毕业的学生中对自己的心理状态选择B的有多少人．

    查看答案和解析>>

    同步练习册答案