
 如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,
如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,分析 (1)把点A(1,2)代入y=kx求出k的值,得出直线y=2x,由直线y=2x与直线y=-2x-5的解析式组成方程组,解方程组即可;
(2)先求出点B的坐标,作CD⊥OB于D,则OB=$\frac{5}{2}$,OD=$\frac{5}{4}$,得出OD=$\frac{1}{2}$OB=BD,由线段垂直平分线的性质得出BC=OC即可.
解答 (1)解:把点A(1,2)代入y=kx得:k=2,
∴直线y=2x,
∵直线y=2x与直线y=-2x-5交于C点,
∴$\left\{\begin{array}{l}{y=2x}\\{y=-2x-5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-\frac{5}{4}}\\{y=-\frac{5}{2}}\end{array}\right.$,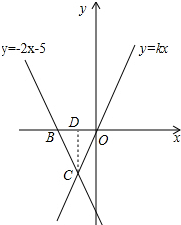
∴点C的坐标为(-$\frac{5}{4}$,-$\frac{5}{2}$);
(2)证明:如图所示:
∵y=-2x-5,
当y=0时,x=-$\frac{5}{2}$,
∴B(-$\frac{5}{2}$,0),
作CD⊥OB于D,则OB=$\frac{5}{2}$,OD=$\frac{5}{4}$,
∴OD=$\frac{1}{2}$OB=BD,
∴BC=OC,
∴△BOC为等腰三角形.
点评 本题考查了直线解析式的求法、两条直线的交点、线段垂直平分线的性质、等腰三角形的判定;求出交点坐标是解决问题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:选择题
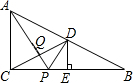 如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )| A. | AQ=$\frac{5}{2}$PQ | B. | AQ=3PQ | C. | AQ=$\frac{8}{3}$PQ | D. | AQ=4PQ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
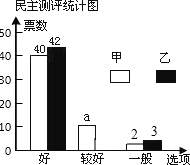 九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:| A | B | C | D | E | |
| 甲 | 89 | 91 | 93 | 94 | 86 |
| 乙 | 88 | 87 | 90 | 98 | 92 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
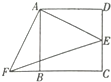 如图,四边形ABCD是正方形,F分别是DC和BC的延长线上的点,且DE=BF,连结AE,AF,EF.
如图,四边形ABCD是正方形,F分别是DC和BC的延长线上的点,且DE=BF,连结AE,AF,EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
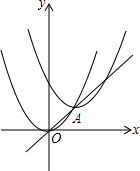 如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )| A. | y=(x+2)2-2 | B. | y=(x+2)2+2 | C. | y=(x-2)2+2 | D. | y=(x-2)2-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
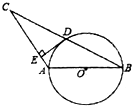 如图,⊙O的直径AB=4,sin∠ABC=$\frac{1}{2}$,BC交⊙O于D,D是BC的中点.
如图,⊙O的直径AB=4,sin∠ABC=$\frac{1}{2}$,BC交⊙O于D,D是BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com