
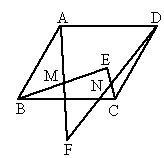
如图所示,AF与BE互相平分,交点为M,EC与DF互相平分,交点为N.求证:四边形ABCD为平行四边形.
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源:新教材完全解读 七年级数学 (下册) (配人教版新课标) (第1次修订版) 配人教版新课标 题型:044
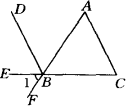
如图所示,AF,CE,DB相交于点B,BE平分∠DBF,且∠1=∠C,问BD与AC平行吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com